Continuity Implies Differentiability - Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If $f$ is a differentiable function at. If f is differentiable at x 0, then f is continuous at x 0. If a function is not continuous at a point, then it is not differentiable there.
If f is differentiable at x 0, then f is continuous at x 0. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If a function is not continuous at a point, then it is not differentiable there. If $f$ is a differentiable function at.
If a function is not continuous at a point, then it is not differentiable there. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If f is differentiable at x 0, then f is continuous at x 0. If $f$ is a differentiable function at.
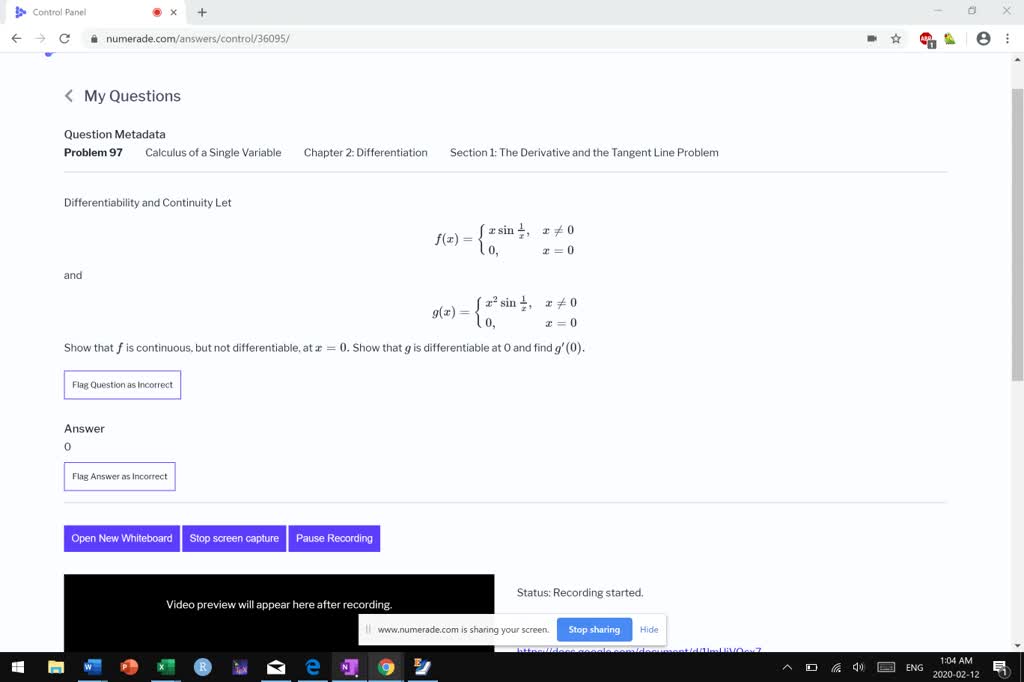
SOLVEDDifferentiability Implies Continuity Use the definition of
If a function is not continuous at a point, then it is not differentiable there. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If $f$ is a differentiable function at. If f is differentiable at x 0, then f is continuous at x 0.
calculus Confirmation of proof that differentiability implies
If f is differentiable at x 0, then f is continuous at x 0. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If $f$ is a differentiable function at. If a function is not continuous at a point, then it is not differentiable there.
derivatives Differentiability Implies Continuity (Multivariable
If $f$ is a differentiable function at. If a function is not continuous at a point, then it is not differentiable there. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If f is differentiable at x 0, then f is continuous at x 0.
Theorem (Differentiability implies Continuity )If f′(x0 ) exists, the f..
If a function is not continuous at a point, then it is not differentiable there. If $f$ is a differentiable function at. If f is differentiable at x 0, then f is continuous at x 0. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability.
Continuity and Differentiability (Fully Explained w/ Examples!)
If f is differentiable at x 0, then f is continuous at x 0. If a function is not continuous at a point, then it is not differentiable there. If $f$ is a differentiable function at. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability.
real analysis Differentiability implies continuity (Linear Map
Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If f is differentiable at x 0, then f is continuous at x 0. If a function is not continuous at a point, then it is not differentiable there. If $f$ is a differentiable function at.
(PDF) An EpsilonDelta Proof That Differentiability Implies Continuity
Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If a function is not continuous at a point, then it is not differentiable there. If f is differentiable at x 0, then f is continuous at x 0. If $f$ is a differentiable function at.
Continuity and Differentiability (Fully Explained w/ Examples!)
If a function is not continuous at a point, then it is not differentiable there. If f is differentiable at x 0, then f is continuous at x 0. If $f$ is a differentiable function at. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability.
derivatives Differentiability Implies Continuity (Multivariable
If $f$ is a differentiable function at. If a function is not continuous at a point, then it is not differentiable there. If f is differentiable at x 0, then f is continuous at x 0. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability.
Theorem (Differentiability implies Continuity )If f′(x0 ) exists, the f..
If f is differentiable at x 0, then f is continuous at x 0. If $f$ is a differentiable function at. Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If a function is not continuous at a point, then it is not differentiable there.
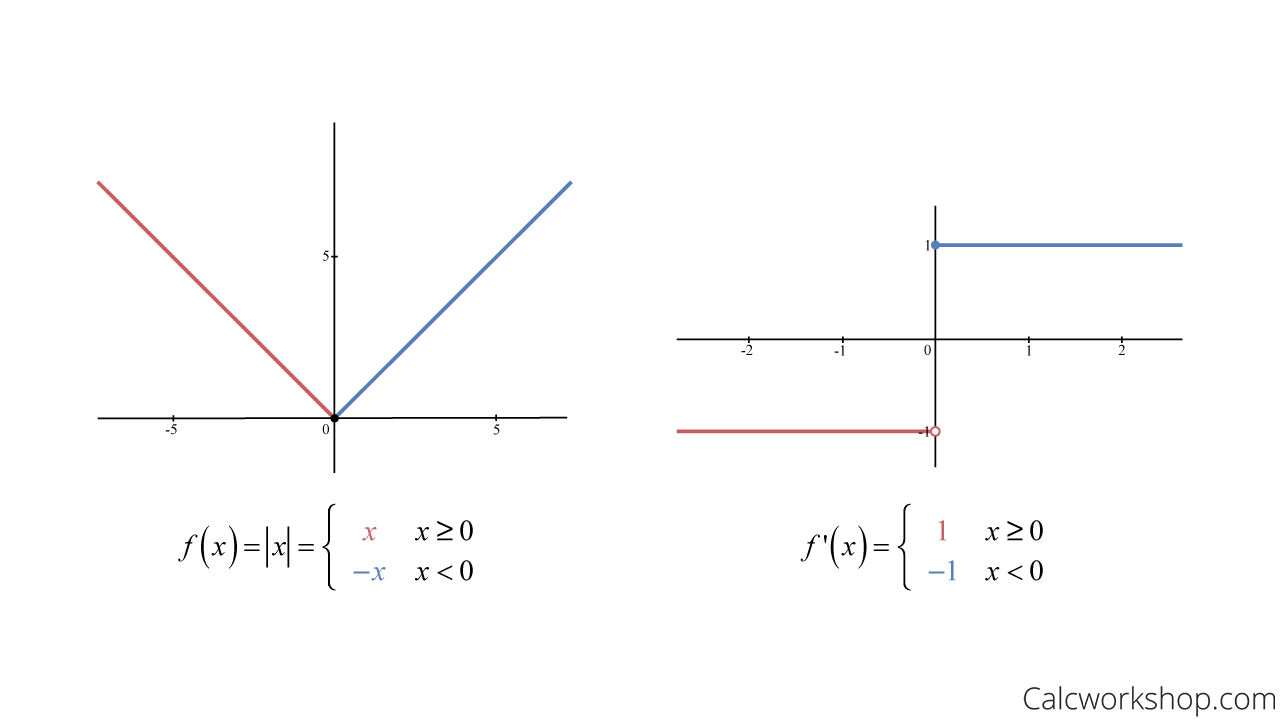
If A Function Is Not Continuous At A Point, Then It Is Not Differentiable There.
Absolute continuity of $f:[a,b] \rightarrow \mathbb{r}$ implies differentiability. If $f$ is a differentiable function at. If f is differentiable at x 0, then f is continuous at x 0.