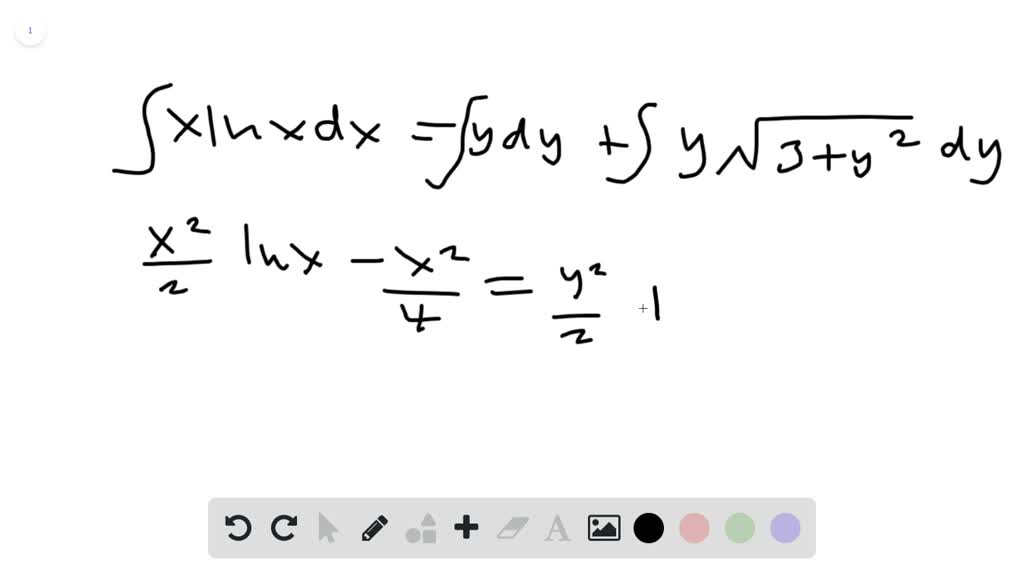Specific Solution Of Differential Given Initial Condition - By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained. An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical methods,. Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution. The calculator will try to find the solution of the given ode:
By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained. The calculator will try to find the solution of the given ode: There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical methods,. An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution.
There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical methods,. The calculator will try to find the solution of the given ode: An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution. By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained.
Solved Find the solution to the differential equation
The calculator will try to find the solution of the given ode: There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical methods,. An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. By using the boundary conditions (also.
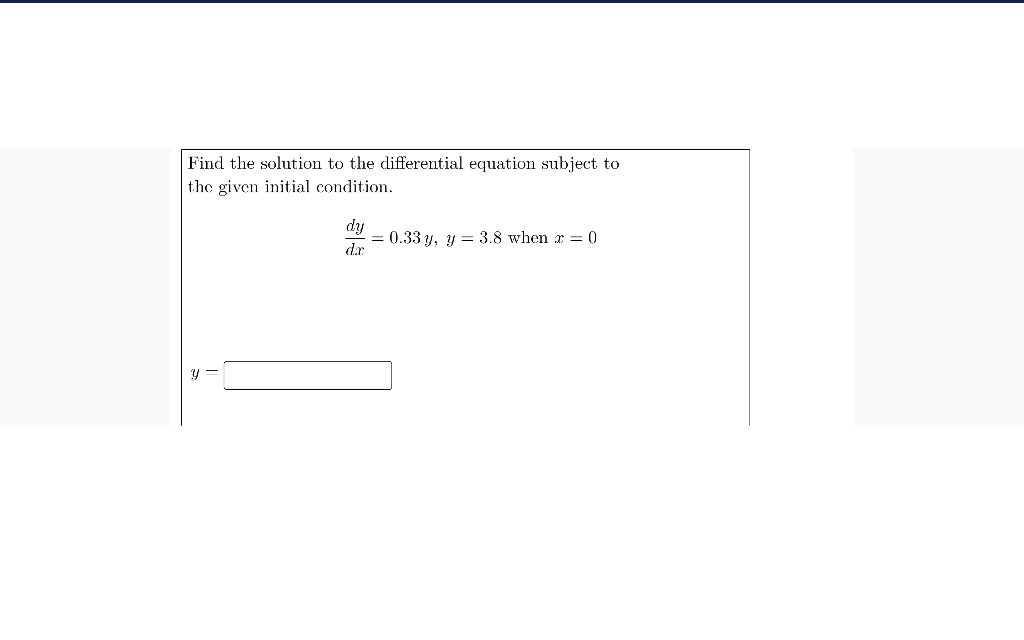
Solved Find the solution to the differential equation below,
Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution. By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained. The calculator will try to find the solution of the given ode: There are several methods that can be used to.
Solved Find the particular solution to the differential
By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained. Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution. An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or.
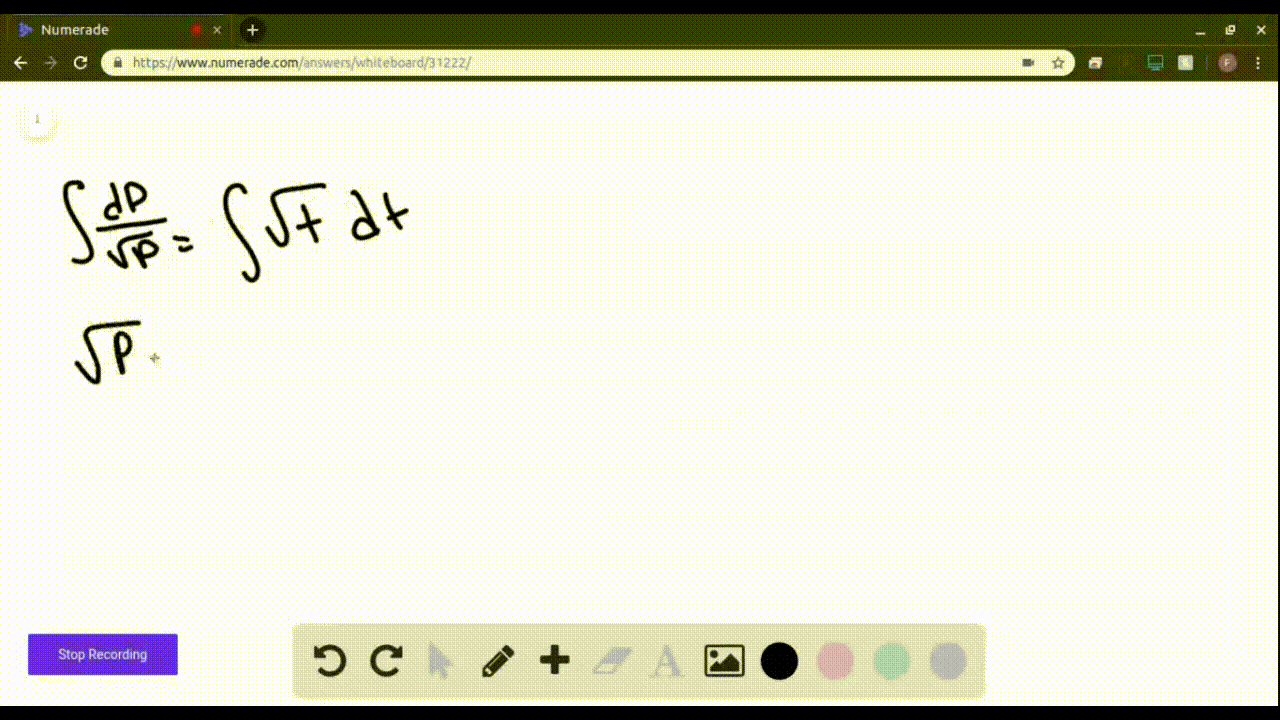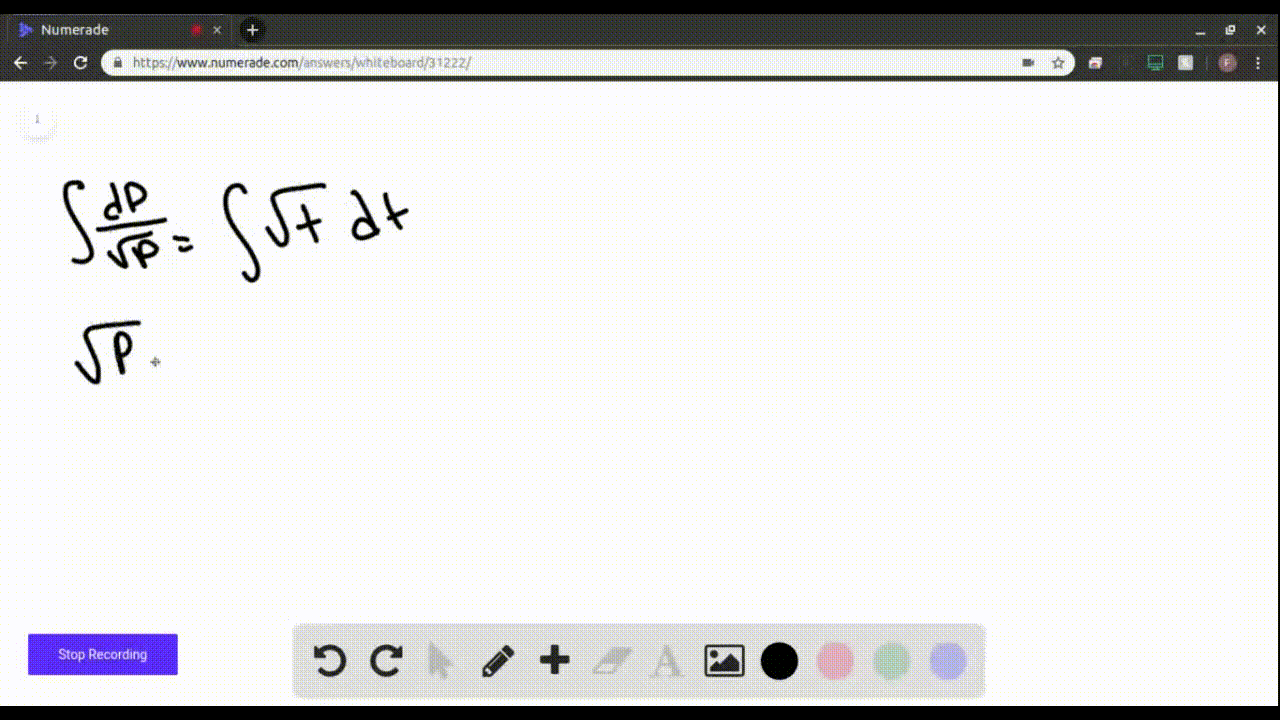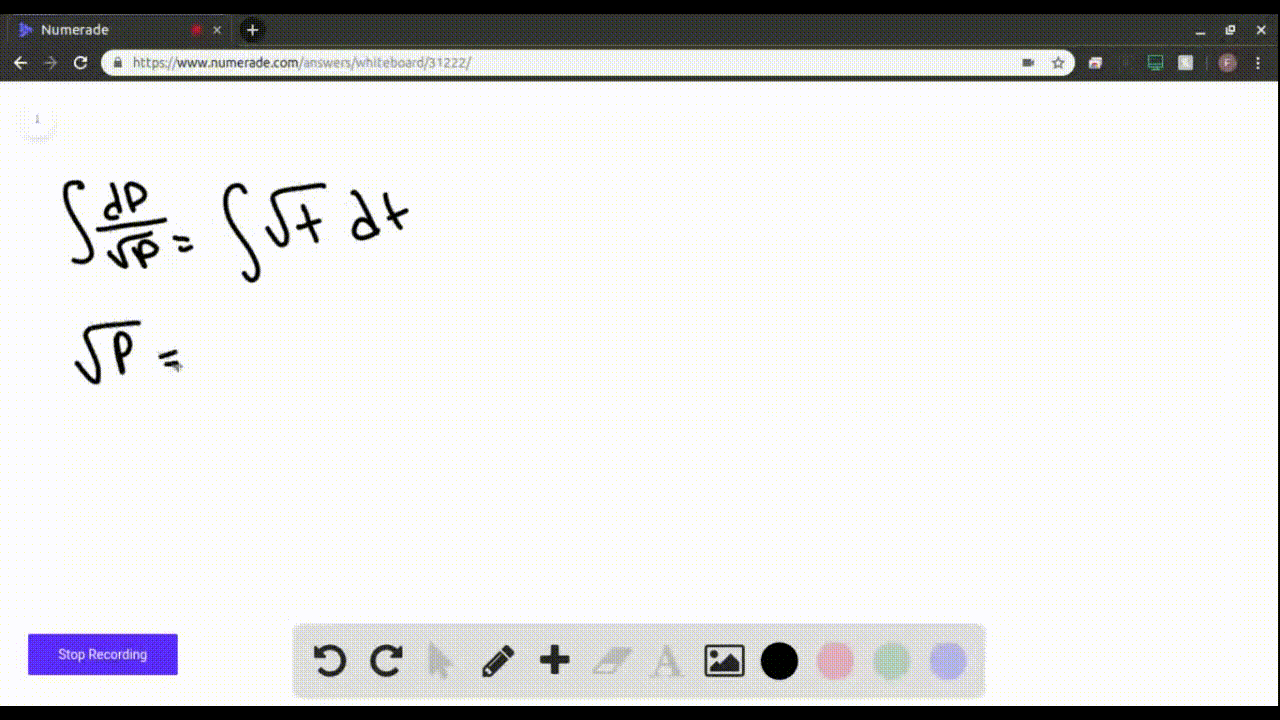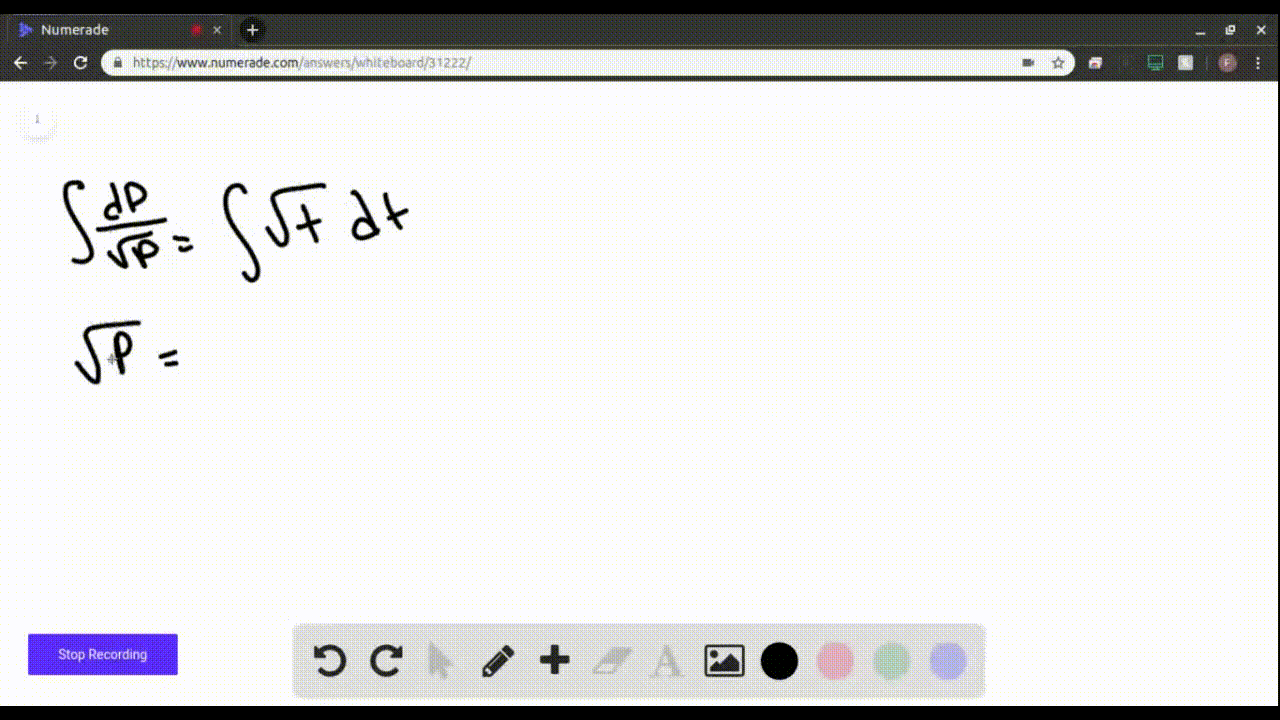
Find the solution of the differential equation that satisfies the given
An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained. Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a.
SOLVEDFind the solution of the differential equation that satisfies
There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical methods,. The calculator will try to find the solution of the given ode: Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution. An initial value problem (ivp) is a differential equations.
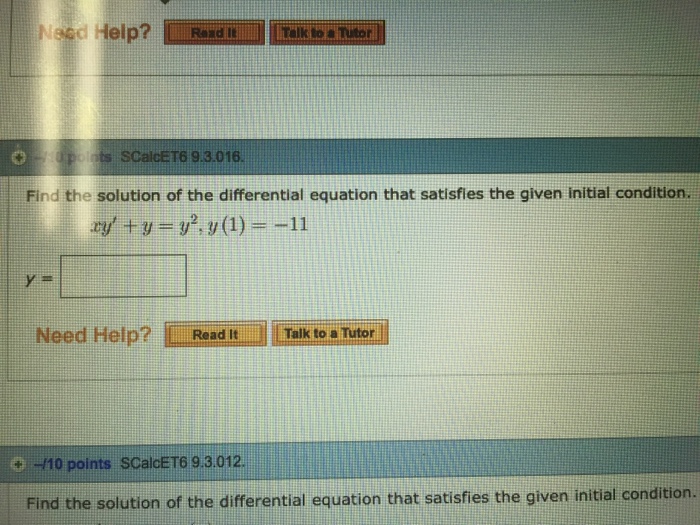
Solved Find the solution of the differential equation that
An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained. There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods,.
Solved Find the solution of the differential equation that
An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution. There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical.
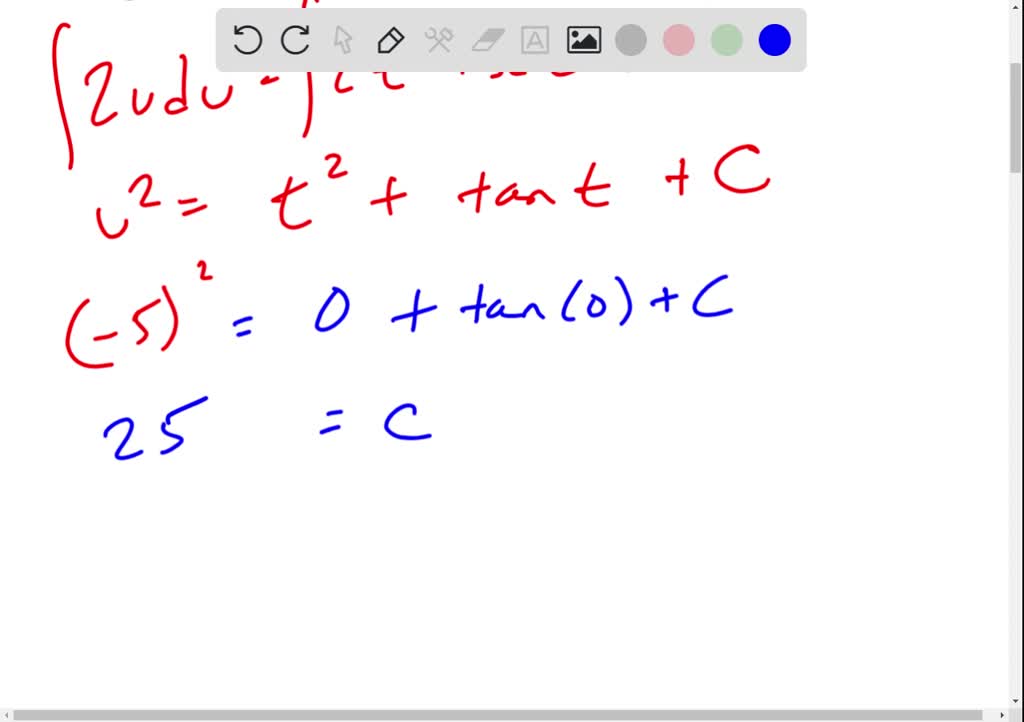
Solved Find the solution to the differential equation
An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution. The calculator will try to find the solution of the given ode: By using the boundary conditions (also known.
⏩SOLVEDFind the solution of the differential equation that… Numerade
There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical methods,. By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained. An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition,.
Solved (a) Find the solution to the differential equation
The calculator will try to find the solution of the given ode: By using the boundary conditions (also known as the initial conditions) the particular solution of a differential equation is obtained. There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical methods,. An initial value problem (ivp) is a differential.
By Using The Boundary Conditions (Also Known As The Initial Conditions) The Particular Solution Of A Differential Equation Is Obtained.
The calculator will try to find the solution of the given ode: An initial value problem (ivp) is a differential equations problem in which we’re asked to use some given initial condition, or set. Given the inhomogeneous linear differential equation, $dx/dt + x = 2t$, use the given ansatz to find a solution. There are several methods that can be used to solve ordinary differential equations (odes) to include analytical methods, numerical methods,.