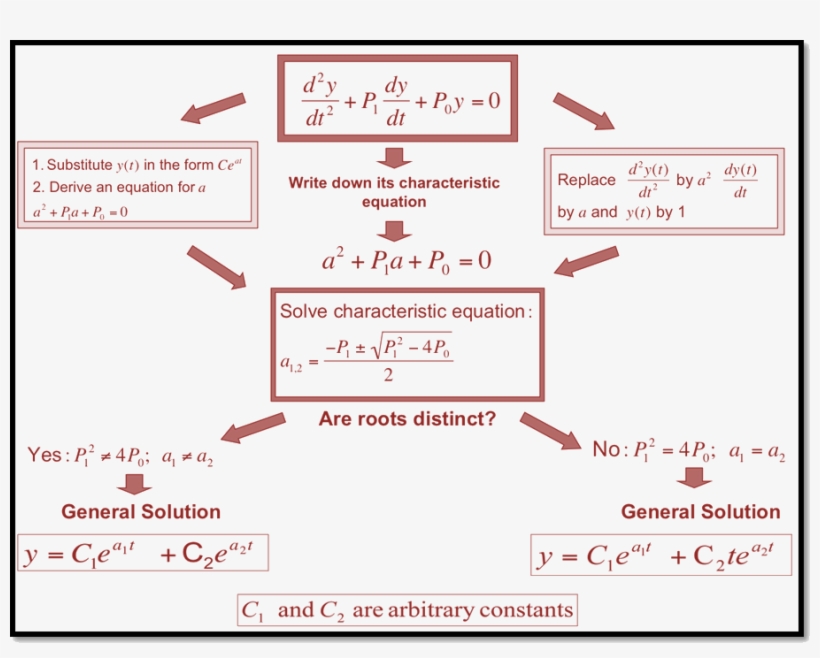
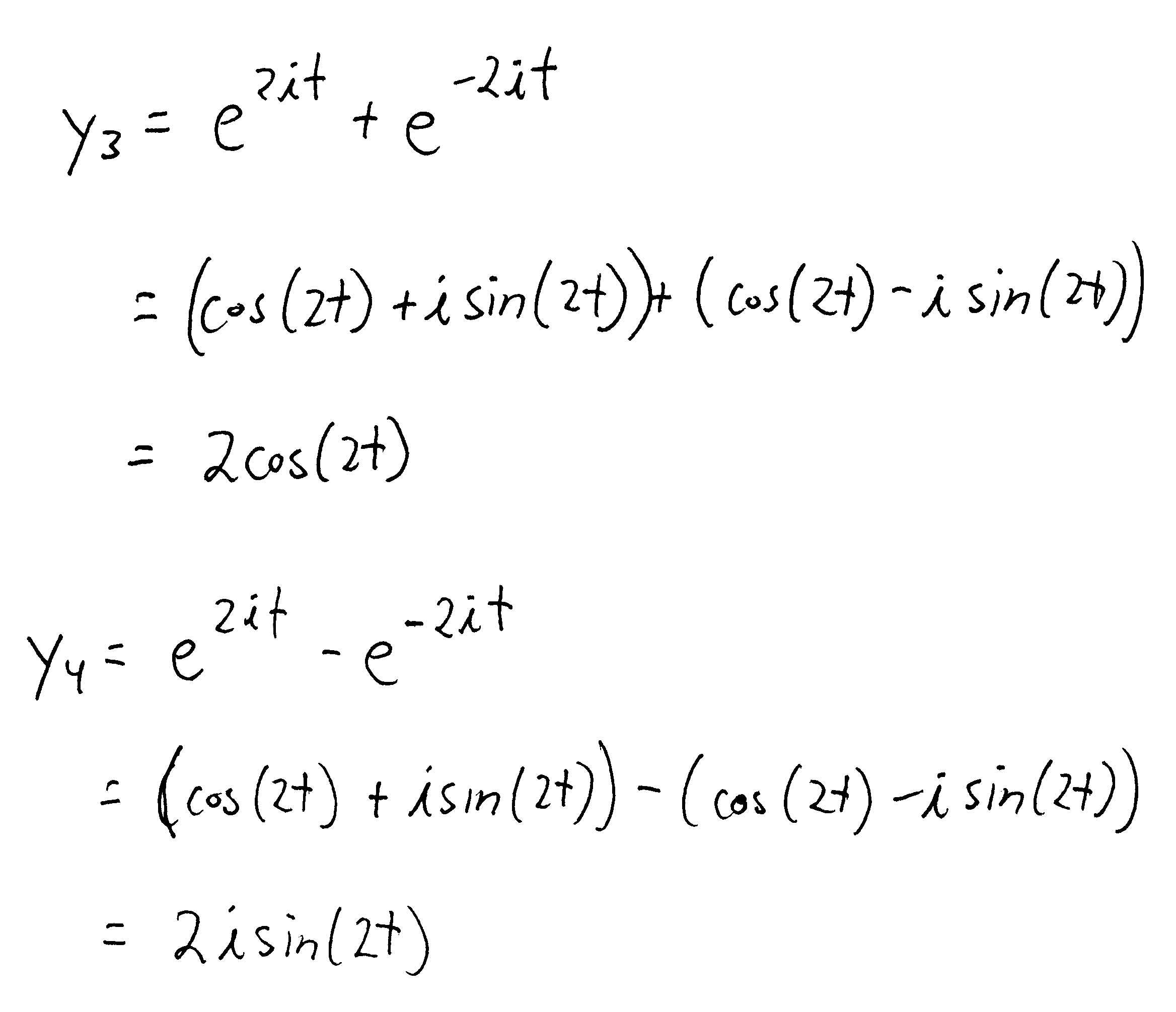Second Order Ordinary Differential Equation Solution

Second Order Ordinary Differential Equation Solution - The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.

Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.

The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.

Finding a second solution to a 2nd order differential equation

The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.

PPT Numerical Solution of Ordinary Differential Equation PowerPoint

Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.

Solved Problem 10.1 FirstOrder Ordinary Differential

Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.

[Solved] The general solution to the secondorder differential equation

Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.

College Park Tutors Blog Differential Equations Solving a second

The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.

First Order Differential Equation Worksheet Equations Worksheets

Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.

Example 4.2.2 (SecondOrder Ordinary Differential

The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.

A Complete Guide to Understanding Second Order Differential Equations

Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.

Solving Second Order Differential Equation Images and Photos finder

Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.

Solution Of Second Order Differential Equation Differential Equation

The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.

The Solution Of These Equations Is Achieved In Stages.

Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.

Related Post:

• How To Prevent Algae In Pond

• Bedsore Prevention Ointment

• Eczema Diagnosis Code

• Nursing Diagnosis For Risk Of Injury

• Example Of Non Linear Differential Equation

• Cat Pneumonia Recovery Time

• Dwyer Differential Pressure Gauge

• N18.6 Diagnosis Code

• How To Prevent Overheating Phone

• C Diff Diagnosis Code

• Second Order Ordinary Differential Equation Solution