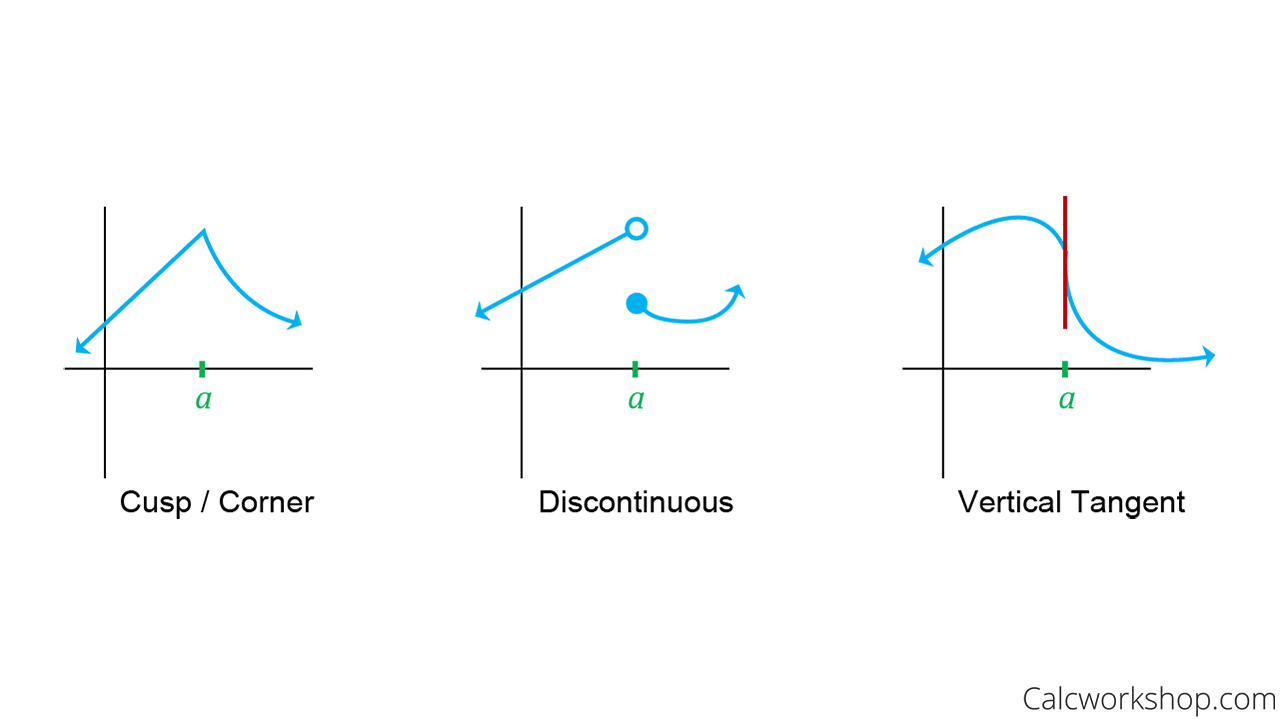
Relationship Between Continuity And Differentiability - How is differentiability different from continuity? Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition.
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability requires that a function has a defined derivative at a point,. How is differentiability different from continuity? Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition.
Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. How is differentiability different from continuity? Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition.
Solved Determine the relationship between differentiability and
How is differentiability different from continuity? Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition.
Worksheet 6 Continuity Differentiability PDF Function (Mathematics
Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. How is differentiability different from continuity? Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by.
CH 3. Continuity Differentiability Differentiation (Math +2) PDF
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability requires that a function has a defined derivative at a point,. Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. How is differentiability different from continuity?
Using GeoGebra to verify the relationship between differentiability and
Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. How is differentiability different from continuity? Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition.
Differentiable vs. Continuous Functions Overview & Relationship
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. How is differentiability different from continuity? Differentiability requires that a function has a defined derivative at a point,.
Continuity and Differentiability (Fully Explained w/ Examples!)
Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability requires that a function has a defined derivative at a point,. Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. How is differentiability different from continuity?
Solved Determine the relationship between differentiability and
How is differentiability different from continuity? Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by.
Continuity and Differentiability (Fully Explained w/ Examples!)
How is differentiability different from continuity? Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. Differentiability requires that a function has a defined derivative at a point,.
Continuity and differentiability
Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. How is differentiability different from continuity? Differentiability requires that a function has a defined derivative at a point,.
3.5 Relationship Between Differentiability and Continuity, and
How is differentiability different from continuity? Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by. Differentiability and continuity are interconnected, with differentiability requiring continuity as a precondition. Differentiability requires that a function has a defined derivative at a point,.
Differentiability And Continuity Are Interconnected, With Differentiability Requiring Continuity As A Precondition.
How is differentiability different from continuity? Differentiability requires that a function has a defined derivative at a point,. Continuity ensures that functions do not have abrupt changes or gaps, while differentiability takes this a step further by.