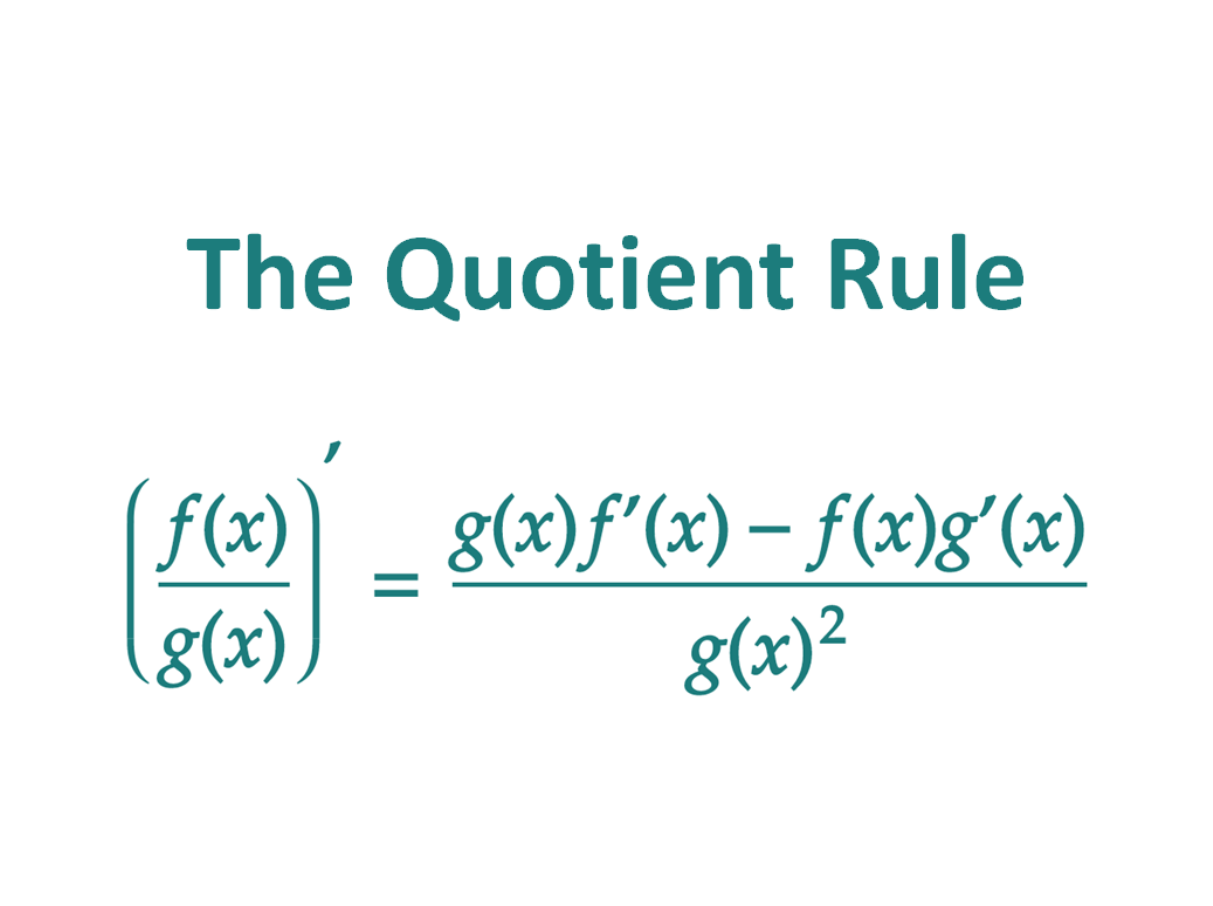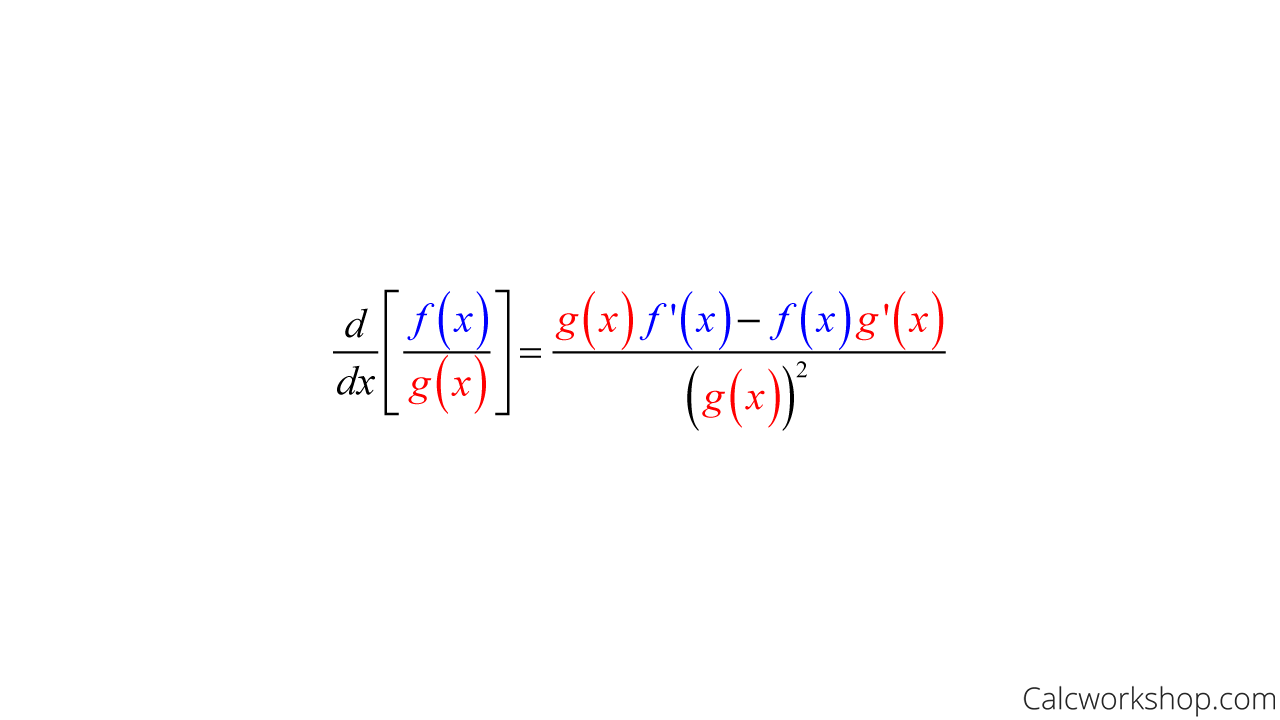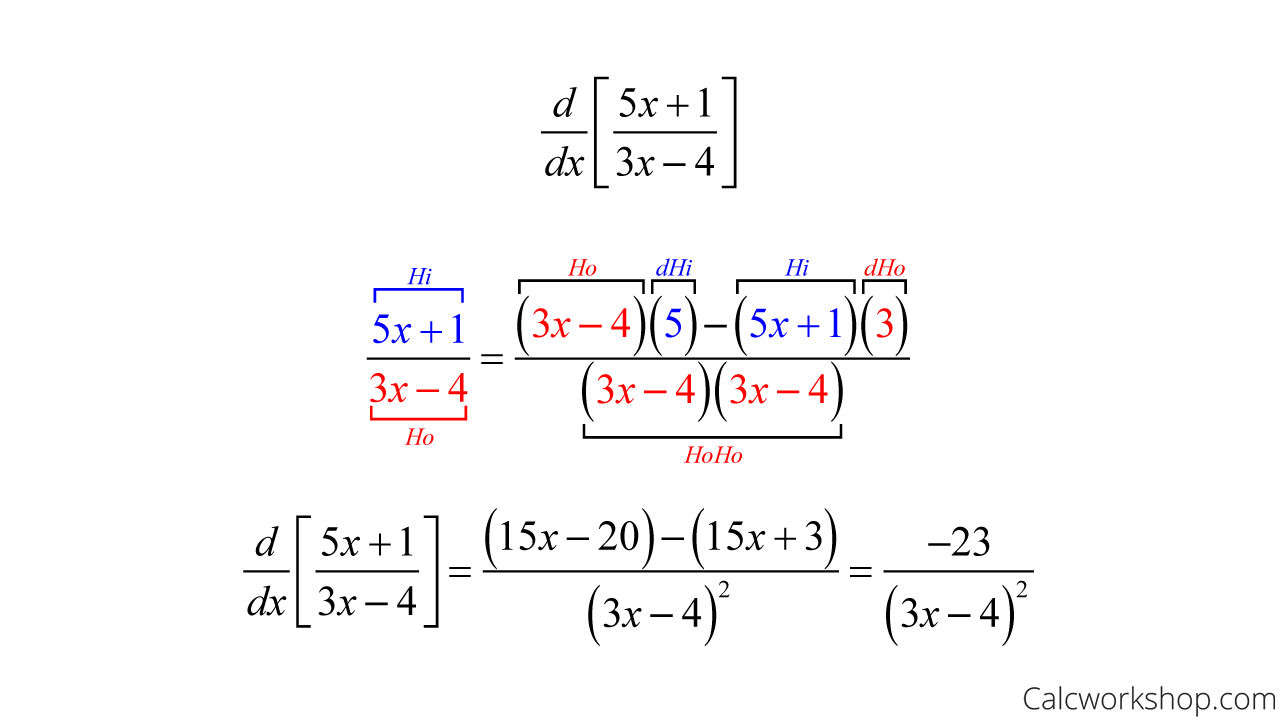Prove The Quotient Rule Of Differentiation - Let h ( x ) = f ( x ) g ( x ). In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k. Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. The quotient rule can be proved either by using the definition of the derivative, or thinking of the quotient \frac {f (x)} {g (x)} as the product f (x). The proof of the quotient rule is shown in the proof of various derivative formulas section of the extras chapter.
The quotient rule can be proved either by using the definition of the derivative, or thinking of the quotient \frac {f (x)} {g (x)} as the product f (x). Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. The proof of the quotient rule is shown in the proof of various derivative formulas section of the extras chapter. In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let h ( x ) = f ( x ) g ( x ). Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k.
In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let h ( x ) = f ( x ) g ( x ). Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k. The quotient rule can be proved either by using the definition of the derivative, or thinking of the quotient \frac {f (x)} {g (x)} as the product f (x). Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. The proof of the quotient rule is shown in the proof of various derivative formulas section of the extras chapter.
The Quotient Rule DerivativeIt
The proof of the quotient rule is shown in the proof of various derivative formulas section of the extras chapter. Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k. In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio.
Using the rule differentiation quotient of two functions, prove that d
Let h ( x ) = f ( x ) g ( x ). Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. The proof of the quotient rule is shown in the proof of various derivative formulas section of the extras chapter. Let ξ ∈ i ξ ∈ i be a.
Differentiation Product & Quotient Rule Kappa Maths Resources for A
The quotient rule can be proved either by using the definition of the derivative, or thinking of the quotient \frac {f (x)} {g (x)} as the product f (x). Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. Let ξ ∈ i ξ ∈ i be a point in i i at.
Differentiation, Quotient rule Teaching Resources
In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k. The quotient rule can be proved either by using the definition of the derivative, or thinking.
Quotient Rule Derivative
Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. The quotient rule can be proved either by using the definition of the derivative, or thinking of the quotient \frac {f (x)} {g (x)} as the product f (x). In calculus, the quotient rule is a method of finding the derivative of a.
Quotient Rule For Calculus (w/ StepbyStep Examples!)
Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k. The quotient rule can be proved either by using the definition of the derivative, or thinking of the quotient \frac {f (x)} {g (x)} as the product f (x). The proof of the quotient rule is shown in the.
Quotient Rule Formula, Definition, Proof, And Examples, 55 OFF
Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k. In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable.
Quotient Rule Differentiation Worksheet
In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k.
vi) Using the rule differentiation quotient of two functions, prove
The quotient rule can be proved either by using the definition of the derivative, or thinking of the quotient \frac {f (x)} {g (x)} as the product f (x). In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let j(x), k(x) j (x), k (x) be.
Quotient Rule Definition
Let h ( x ) = f ( x ) g ( x ). Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k. In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let j(x),.
The Proof Of The Quotient Rule Is Shown In The Proof Of Various Derivative Formulas Section Of The Extras Chapter.
Let j(x), k(x) j (x), k (x) be real functions defined on the open interval i i. In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. The quotient rule can be proved either by using the definition of the derivative, or thinking of the quotient \frac {f (x)} {g (x)} as the product f (x). Let ξ ∈ i ξ ∈ i be a point in i i at which both j j and k k.