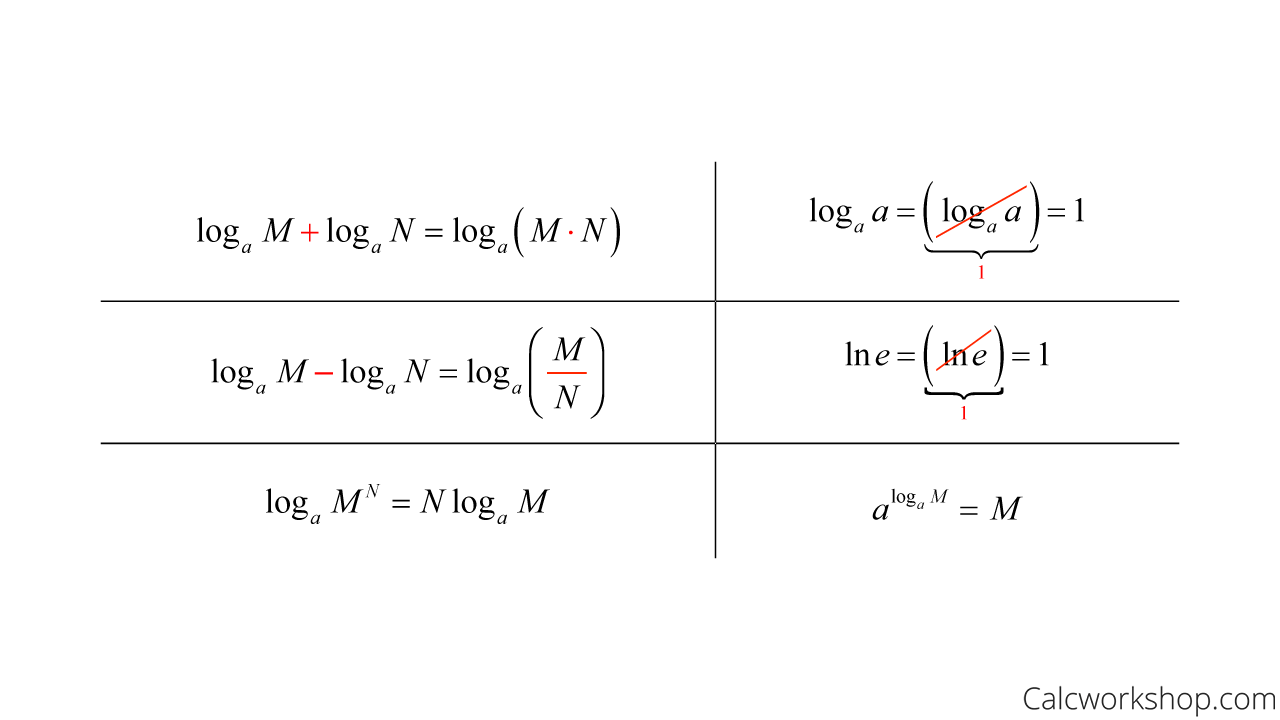
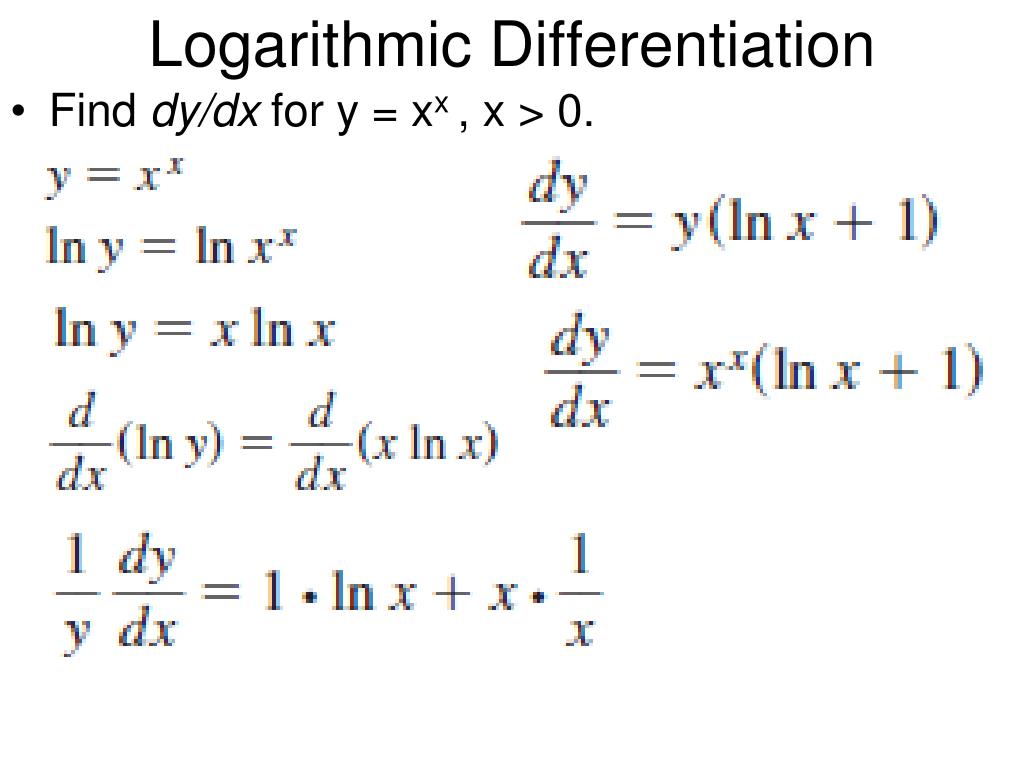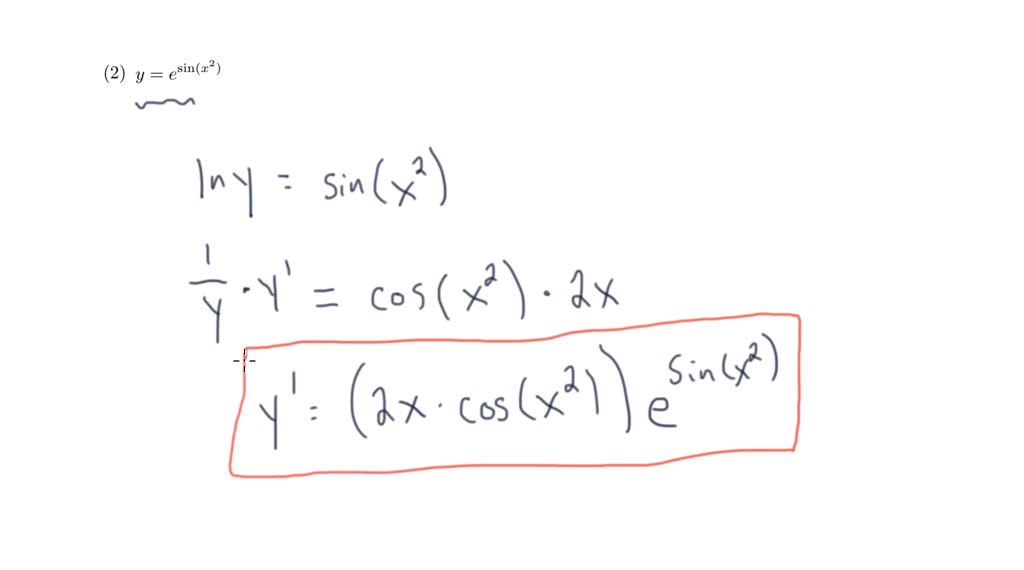Log Differentiation - Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base e) to transform products into sums and. Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of. Logarithmic differentiation gives an alternative method for differentiating products and quotients. Learn more about the derivative of log x along with its proof using. In this section we will discuss logarithmic differentiation. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by taking the natural logarithm of both sides and. The derivative of log x is 1/(x ln 10) and the derivative of log x with base a is 1/(x ln a) and the derivative of ln x is 1/x.
Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base e) to transform products into sums and. Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of. The derivative of log x is 1/(x ln 10) and the derivative of log x with base a is 1/(x ln a) and the derivative of ln x is 1/x. In this section we will discuss logarithmic differentiation. Learn more about the derivative of log x along with its proof using. Logarithmic differentiation gives an alternative method for differentiating products and quotients. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by taking the natural logarithm of both sides and.
Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base e) to transform products into sums and. Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of. Logarithmic differentiation gives an alternative method for differentiating products and quotients. In this section we will discuss logarithmic differentiation. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by taking the natural logarithm of both sides and. Learn more about the derivative of log x along with its proof using. The derivative of log x is 1/(x ln 10) and the derivative of log x with base a is 1/(x ln a) and the derivative of ln x is 1/x.
ShowMe logarithmic differentiation
Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base e) to transform products into sums and. Learn more about the derivative of log x along with its proof using. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by.
Differentiation Of Log X Derivatives of Logs YouTube Find if y
Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by taking the natural logarithm of both sides and. The derivative of log x is 1/(x ln 10) and the derivative of log x with base a is 1/(x ln a) and the derivative of ln x is 1/x. Learn more about the derivative of.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
Logarithmic differentiation gives an alternative method for differentiating products and quotients. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by taking the natural logarithm of both sides and. Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function.
Log Y Differentiation at Jeremy Broady blog
Learn more about the derivative of log x along with its proof using. Logarithmic differentiation gives an alternative method for differentiating products and quotients. Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of. Logarithmic differentiation relies on the chain rule as.
Log Y Differentiation at Jeremy Broady blog
Logarithmic differentiation gives an alternative method for differentiating products and quotients. Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of. Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm.
Differentiation Of Log X Derivatives of Logs YouTube Find if y
In this section we will discuss logarithmic differentiation. Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base e) to transform products into sums and. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by taking the natural logarithm of.
Question Video Logarithmic Differentiation Of Functions, 40 OFF
Learn more about the derivative of log x along with its proof using. Logarithmic differentiation gives an alternative method for differentiating products and quotients. Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of. Logarithmic differentiation relies on the chain rule as.
Question Video Logarithmic Differentiation Of Functions, 40 OFF
Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of. In this section we will discuss logarithmic differentiation. Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base.
Logarithmic differentiation example 1 Numerade
Learn more about the derivative of log x along with its proof using. Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base e) to transform products into sums and. In this section we will discuss logarithmic differentiation. Logarithmic differentiation allows us to differentiate functions of.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
Learn more about the derivative of log x along with its proof using. Logarithmic differentiation gives an alternative method for differentiating products and quotients. Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base e) to transform products into sums and. The derivative of log x.
Learn More About The Derivative Of Log X Along With Its Proof Using.
Logarithmic differentiation relies on the chain rule as well as properties of logarithms (in particular, the natural logarithm, or the logarithm to the base e) to transform products into sums and. The derivative of log x is 1/(x ln 10) and the derivative of log x with base a is 1/(x ln a) and the derivative of ln x is 1/x. Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of. In this section we will discuss logarithmic differentiation.
Logarithmic Differentiation Allows Us To Differentiate Functions Of The Form \(Y=G(X)^{F(X)}\) Or Very Complex Functions By Taking The Natural Logarithm Of Both Sides And.
Logarithmic differentiation gives an alternative method for differentiating products and quotients.