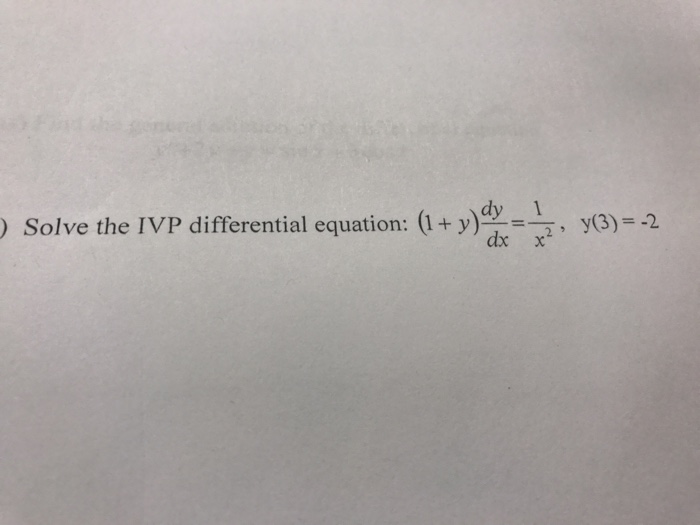Ivp Differential Equation - In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[ ← pde ⎬ u = u 0 on ω ×{0} ← initial condition u =. In the context of problems where the dependent variable is time, an initial condition. Having explored the laplace transform, its inverse, and its properties, we are now equipped.
Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[ ← pde ⎬ u = u 0 on ω ×{0} ← initial condition u =. Having explored the laplace transform, its inverse, and its properties, we are now equipped. In the context of problems where the dependent variable is time, an initial condition. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of.
Having explored the laplace transform, its inverse, and its properties, we are now equipped. In the context of problems where the dependent variable is time, an initial condition. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[ ← pde ⎬ u = u 0 on ω ×{0} ← initial condition u =.
IVP to BVP Differential Equation parametric transformation. Download
In the context of problems where the dependent variable is time, an initial condition. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[ ← pde ⎬ u = u 0 on ω ×{0} ← initial condition u =. Having explored the laplace transform, its inverse, and its properties, we are now equipped. In this chapter.
Differential equation systems solver matrix survivalsay
Having explored the laplace transform, its inverse, and its properties, we are now equipped. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. In the context of problems where the dependent variable is time, an initial condition. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[.
Solved J 1. Solve each differential equation or IVP a. xy'
In the context of problems where the dependent variable is time, an initial condition. Having explored the laplace transform, its inverse, and its properties, we are now equipped. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[.
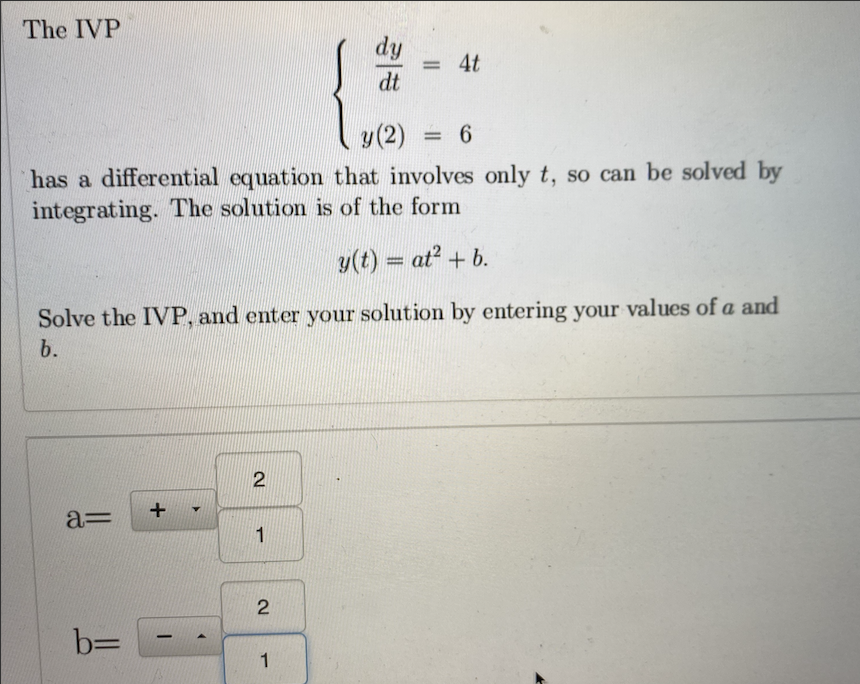
Solved The IVP a = 4t y(2) = 6 has a differential equation
Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[ ← pde ⎬ u = u 0 on ω ×{0} ← initial condition u =. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. In the context of problems where the dependent variable is time, an initial.
Solved Solve The Following Differential Equation On IVP Y...
Having explored the laplace transform, its inverse, and its properties, we are now equipped. In the context of problems where the dependent variable is time, an initial condition. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[.
Solving IVP With Laplace Transforms PDF Ordinary Differential
Having explored the laplace transform, its inverse, and its properties, we are now equipped. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. In the context of problems where the dependent variable is time, an initial condition. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[.
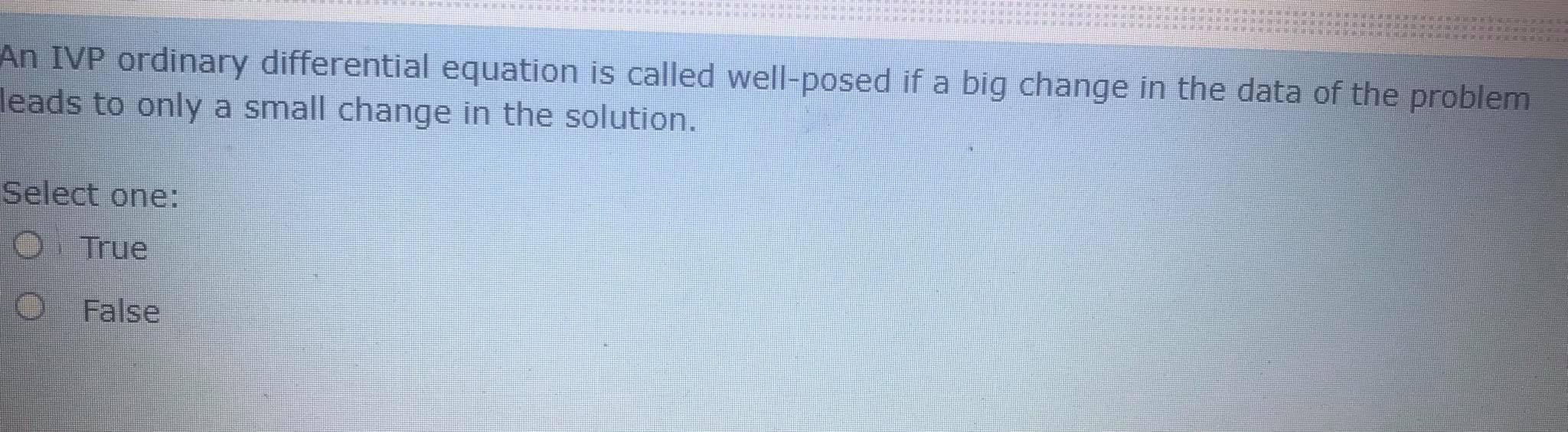
Solved An IVP ordinary differential equation is called
In the context of problems where the dependent variable is time, an initial condition. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[ ← pde ⎬ u = u 0 on ω ×{0} ← initial condition u =. Having explored the laplace transform, its inverse, and its properties, we are now equipped. In this chapter.
Solved Solve the IVP differential equation (1 + y) dy/dx =
In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[ ← pde ⎬ u = u 0 on ω ×{0} ← initial condition u =. Having explored the laplace transform, its inverse, and its properties, we are now.
Solved on 21 An IVP ordinary differential equation is called
Having explored the laplace transform, its inverse, and its properties, we are now equipped. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. In the context of problems where the dependent variable is time, an initial condition. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[.
Find a solution of the secondorder IVP consisting of
Having explored the laplace transform, its inverse, and its properties, we are now equipped. In the context of problems where the dependent variable is time, an initial condition. In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[.
In The Context Of Problems Where The Dependent Variable Is Time, An Initial Condition.
In this chapter we introduce the notion of an initial value problem (ivp) for first order systems of. Initial value problems (ivp) ⎧ ⎨ ⎩ ⎫ u t = lu in ω×]0,t[ ← pde ⎬ u = u 0 on ω ×{0} ← initial condition u =. Having explored the laplace transform, its inverse, and its properties, we are now equipped.