Is Absolute Value Differentiable - Let |x| be the absolute value of x for real x. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. Let u be a differentiable. **no, the absolute value function is not.
Let |x| be the absolute value of x for real x. Let u be a differentiable. **no, the absolute value function is not. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere.
**no, the absolute value function is not. Let u be a differentiable. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. Let |x| be the absolute value of x for real x.
Absolute Value Write A Topic
$\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. Let |x| be the absolute value of x for real x. **no, the absolute value function is not. Let u be a differentiable.
Are Fractals or Fractal Curves Differentiable?
Let u be a differentiable. Let |x| be the absolute value of x for real x. **no, the absolute value function is not. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere.
Why is the absolute value function not differentiable at 0 Quizlet
Let |x| be the absolute value of x for real x. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. Let u be a differentiable. **no, the absolute value function is not.
Differentiable Cuemath
**no, the absolute value function is not. Let |x| be the absolute value of x for real x. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. Let u be a differentiable.
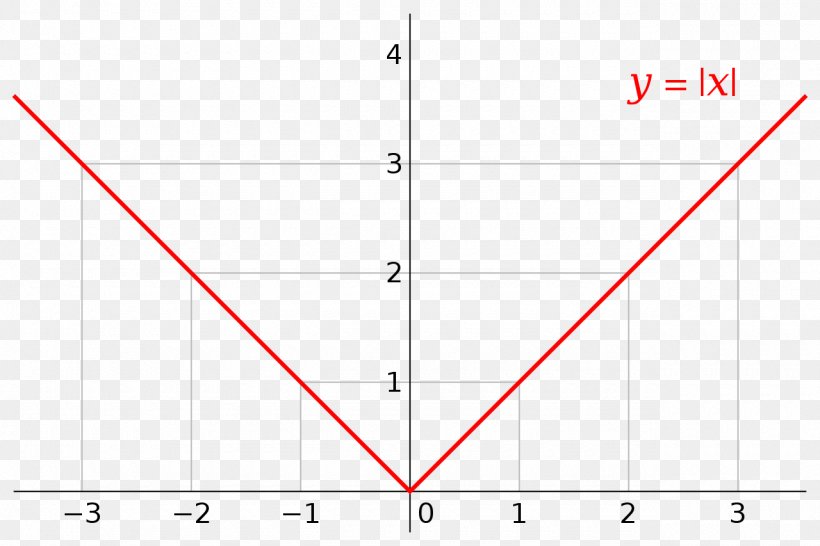
Absolute Value Graph Of A Function Differentiable Function Real Number
$\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. Let |x| be the absolute value of x for real x. Let u be a differentiable. **no, the absolute value function is not.
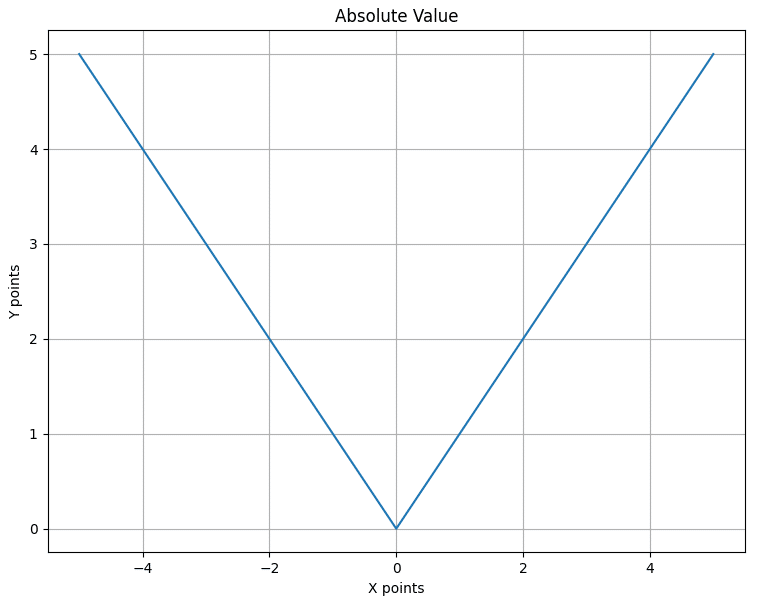
Absolute value is differentiable everywhere except the corner point
**no, the absolute value function is not. Let |x| be the absolute value of x for real x. Let u be a differentiable. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere.
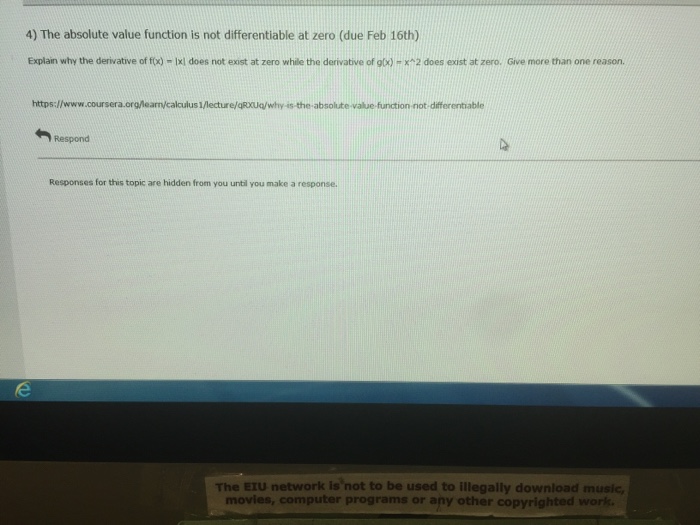
Solved 4) The absolute value function is not differentiable
$\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. Let |x| be the absolute value of x for real x. Let u be a differentiable. **no, the absolute value function is not.
calculus Differentiable approximation of the absolute value function
Let u be a differentiable. **no, the absolute value function is not. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. Let |x| be the absolute value of x for real x.
Absolute Value Nutshell
Let u be a differentiable. Let |x| be the absolute value of x for real x. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. **no, the absolute value function is not.
Flexi answers Is the absolute value differentiable? CK12 Foundation
**no, the absolute value function is not. Let |x| be the absolute value of x for real x. Let u be a differentiable. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere.
Let U Be A Differentiable.
Let |x| be the absolute value of x for real x. $\begingroup$ sure, $f(x) = x^2\sin(1/x)$ (when $x\neq 0$, and $f(0)=0$) is everywhere. **no, the absolute value function is not.