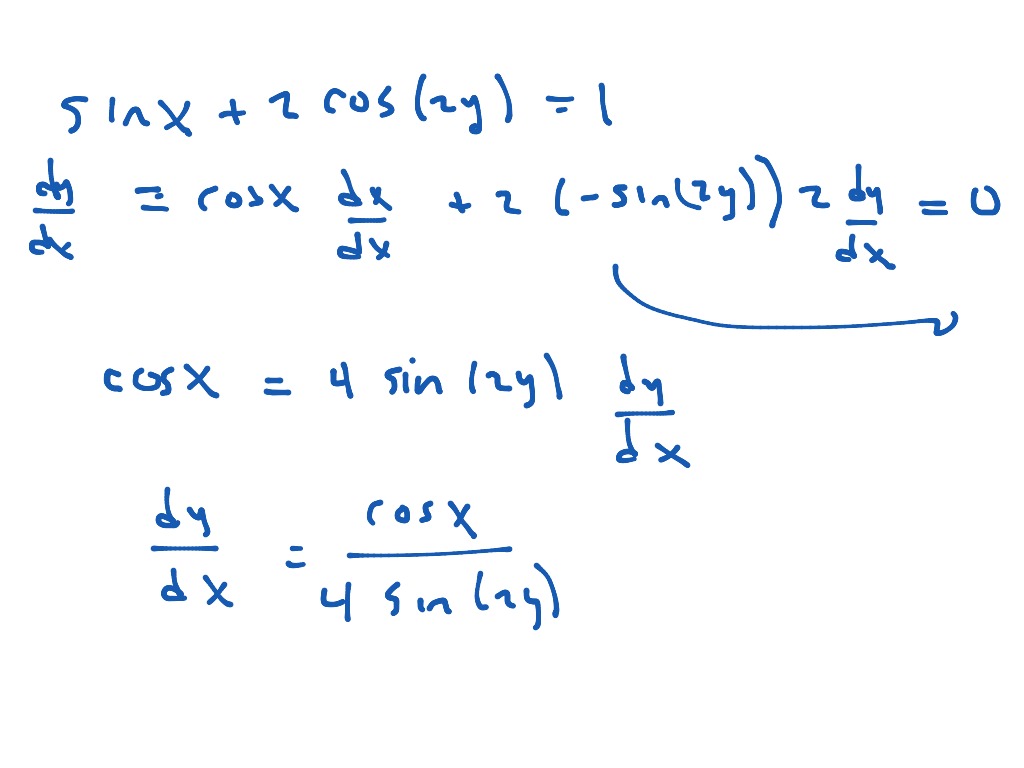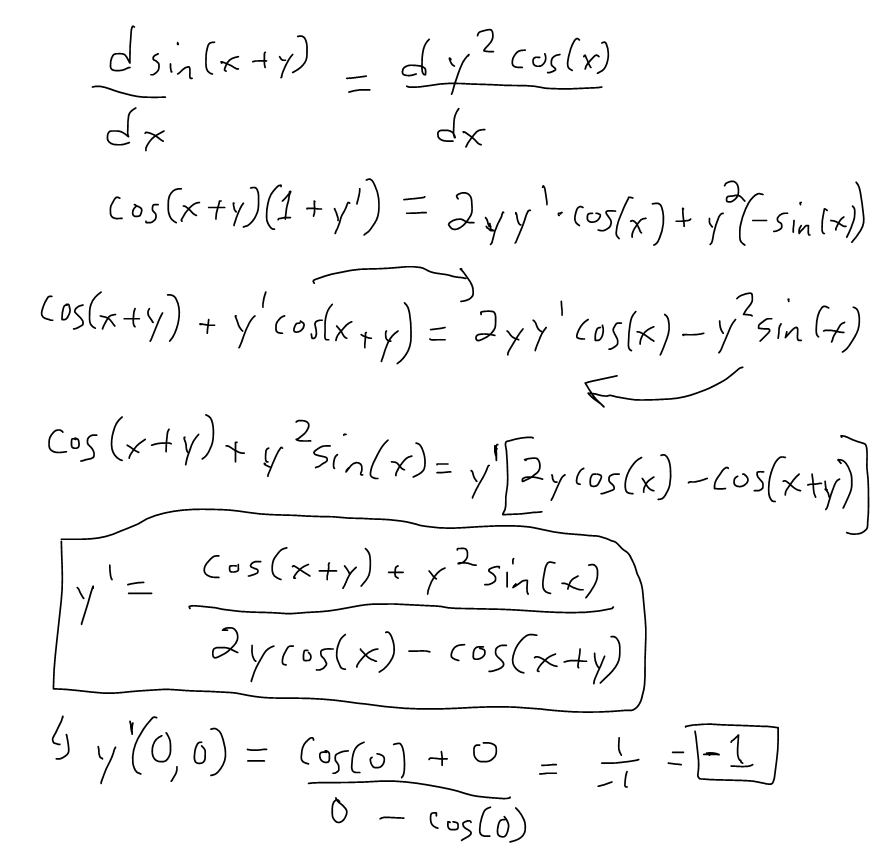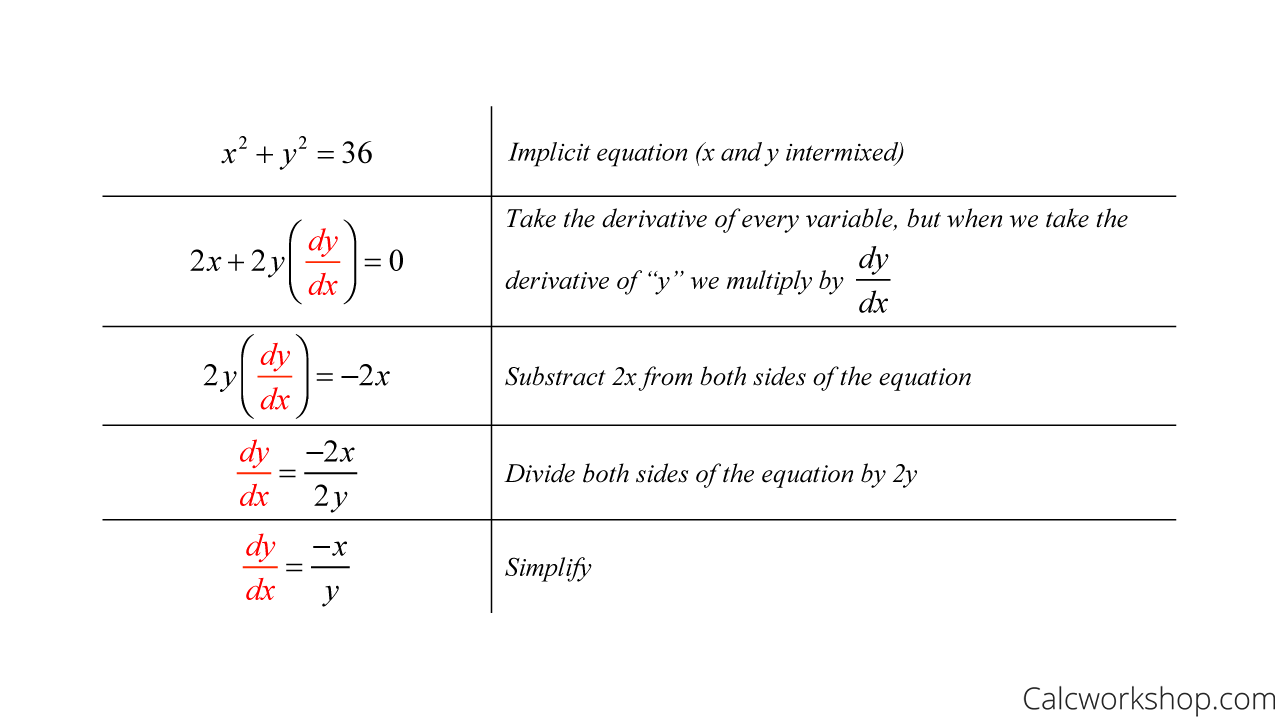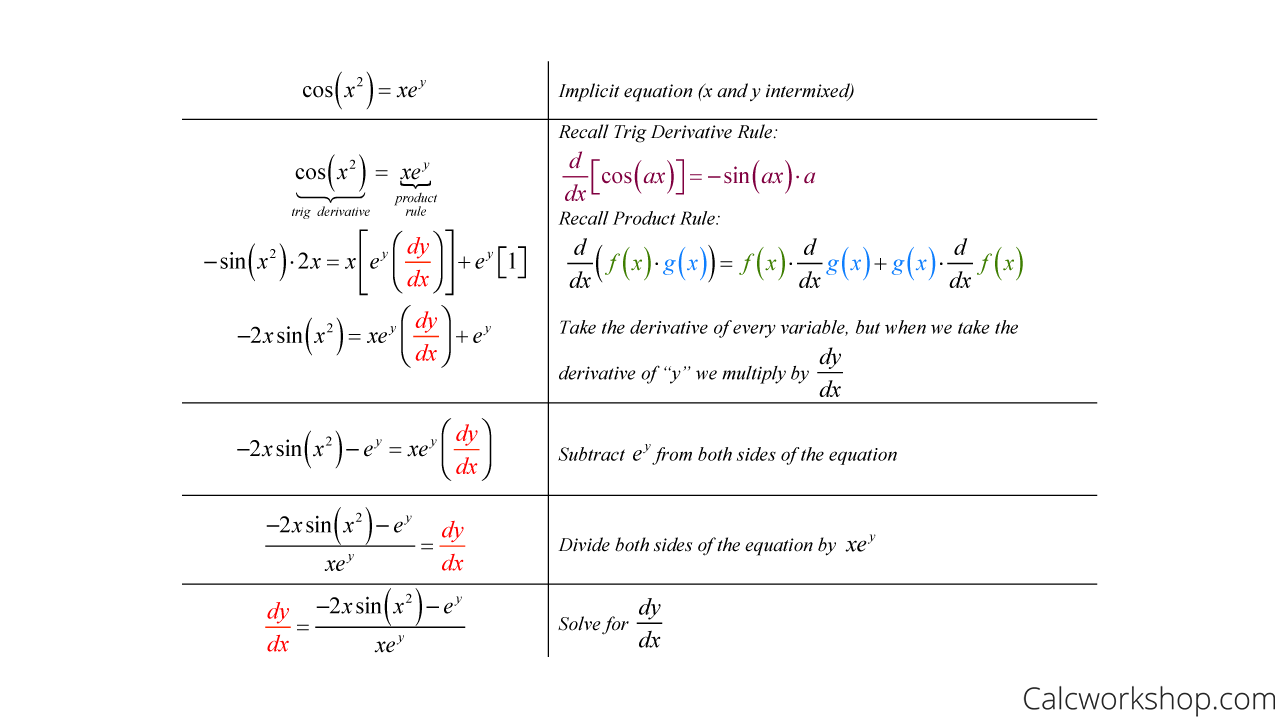Implicit Differentiation Trig Functions - First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. Find \(y'\) by solving the equation for y and differentiating directly. In this unit we study how to differentiate a function given in this form.
First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. In this unit we study how to differentiate a function given in this form. Find \(y'\) by solving the equation for y and differentiating directly.
Find \(y'\) by solving the equation for y and differentiating directly. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. In this unit we study how to differentiate a function given in this form. First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$.
![Trig Identities Derivatives [Inverse, Antiderivative]](https://trigidentities.net/wp-content/uploads/2022/10/Inverse-Trig-Identities-Derivatives-1024x888.jpg)
Trig Identities Derivatives [Inverse, Antiderivative]
For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. Find \(y'\) by solving the equation for y and differentiating directly. In this unit we study how to differentiate a function given in this form. First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$.
Implicit Differentiation and Inverse Trig Functions NoraCuranaj
In this unit we study how to differentiate a function given in this form. First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. Find \(y'\) by solving the equation for y and differentiating directly.
ShowMe differentiation trig
First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. Find \(y'\) by solving the equation for y and differentiating directly. In this unit we study how to differentiate a function given in this form.
Implicit Differentiation Example on Trigonometry PeakD
For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. Find \(y'\) by solving the equation for y and differentiating directly. In this unit we study how to differentiate a function given in this form. First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$.
Implicit Differentiation (w/ Examples And Worksheets!)
First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. Find \(y'\) by solving the equation for y and differentiating directly. In this unit we study how to differentiate a function given in this form. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x.
Implicit Differentiation Inverse Trig Math 115, Implicit
Find \(y'\) by solving the equation for y and differentiating directly. First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. In this unit we study how to differentiate a function given in this form. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x.
Implicit Differentiation W Examples And Worksheets 25000 Hot Sex Picture
First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. In this unit we study how to differentiate a function given in this form. Find \(y'\) by solving the equation for y and differentiating directly. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x.
Implicit Differentiation (w/ Examples And Worksheets!)
First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. Find \(y'\) by solving the equation for y and differentiating directly. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. In this unit we study how to differentiate a function given in this form.
Implicit Differentiation Calculus Study guide
First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. In this unit we study how to differentiate a function given in this form. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. Find \(y'\) by solving the equation for y and differentiating directly.
Implicit Differentiation Practice Quiz
First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. In this unit we study how to differentiate a function given in this form. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x. Find \(y'\) by solving the equation for y and differentiating directly.
In This Unit We Study How To Differentiate A Function Given In This Form.
Find \(y'\) by solving the equation for y and differentiating directly. First, you should be writing $\frac{d}{dx}$, not $\frac{dy}{dx}$. For the chain rule, you want to multiply cos(y − 2x) cos (y − 2 x) by the derivative of y − 2x y − 2 x.