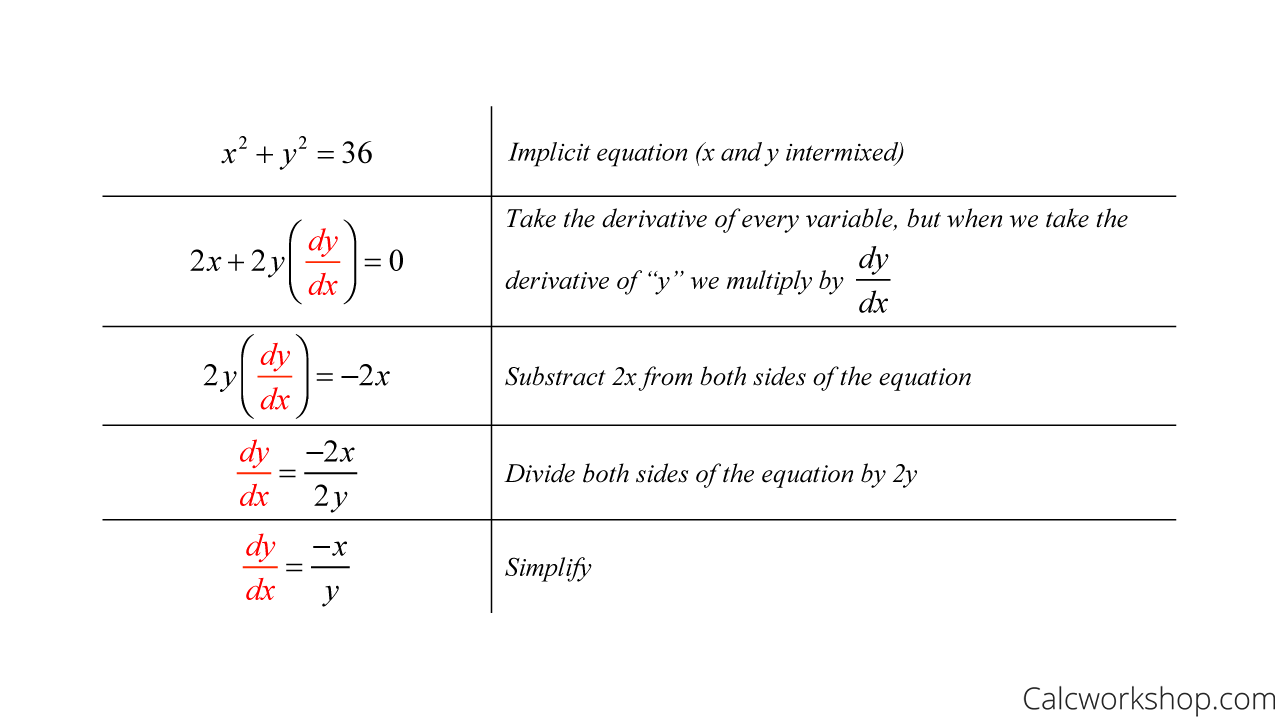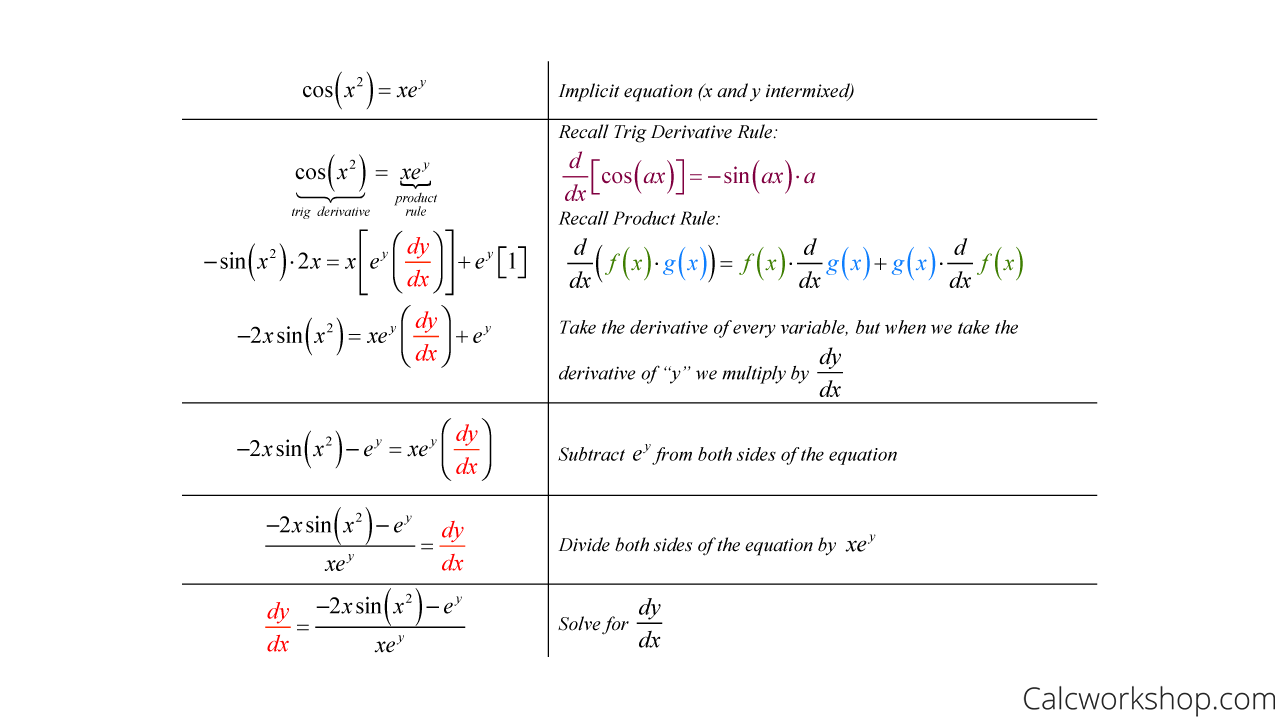Implicit Differentiation Of Partial Derivatives - There are some situations when we have an equation implicitly defining a surface (meaning. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Now let's try implicit differentiation: Partially differentiating both sides with respect to x: Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. So, if you can do calculus i derivatives you shouldn’t have too much. Perform implicit differentiation of a function of two or more variables. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Z are related implicitly if they depend on each other by an equation of the.
Perform implicit differentiation of a function of two or more variables. Partially differentiating both sides with respect to x: Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Z are related implicitly if they depend on each other by an equation of the. So, if you can do calculus i derivatives you shouldn’t have too much. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. There are some situations when we have an equation implicitly defining a surface (meaning. Now let's try implicit differentiation:
$$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Partially differentiating both sides with respect to x: Z are related implicitly if they depend on each other by an equation of the. Now let's try implicit differentiation: So, if you can do calculus i derivatives you shouldn’t have too much. There are some situations when we have an equation implicitly defining a surface (meaning. Perform implicit differentiation of a function of two or more variables. Fortunately, the concept of implicit differentiation for derivatives of single variable functions can.
SOLUTION partial differentiation , partial derivatives , implicit
Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Z are related implicitly if they depend on each other by an equation of the. Perform implicit differentiation of a function of two or more variables. $$ $$ 2x y^4.
SOLUTION partial differentiation , partial derivatives , implicit
So, if you can do calculus i derivatives you shouldn’t have too much. Now let's try implicit differentiation: $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Perform implicit differentiation of a function of two or more variables. Fortunately, the concept of implicit differentiation for derivatives of single variable functions can.
SOLUTION partial differentiation , partial derivatives , implicit
So, if you can do calculus i derivatives you shouldn’t have too much. Perform implicit differentiation of a function of two or more variables. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Z are related implicitly if they depend on each other by an equation of the. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x.
calculus Implicit Partial Differentiation Mathematics Stack Exchange
$$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. There are some situations when we have an equation implicitly defining a surface (meaning. Partially differentiating both sides with respect to x: Perform implicit differentiation of a function of two or more variables.
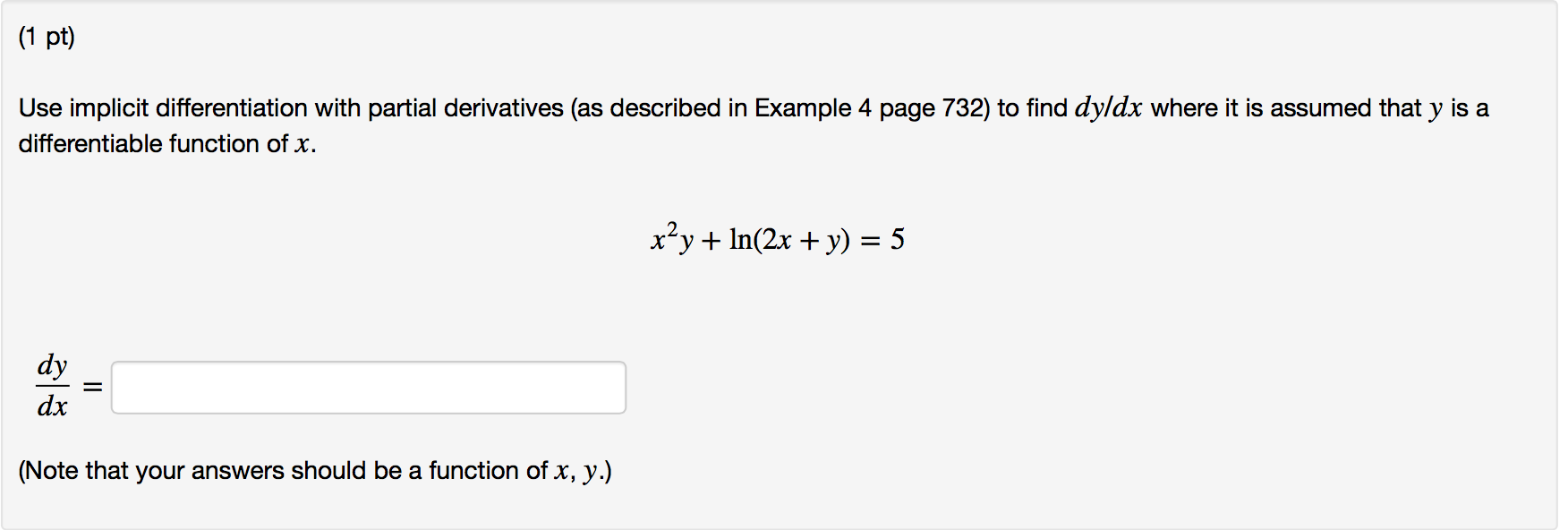
Solved Use implicit differentiation with partial derivatives
Now let's try implicit differentiation: There are some situations when we have an equation implicitly defining a surface (meaning. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. Perform implicit differentiation of a function of two or more variables. So, if you can do calculus i derivatives you shouldn’t have too much.
multivariable calculus Implicit differentiation with partial
Now let's try implicit differentiation: Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. So, if you can do calculus i derivatives you shouldn’t have too much. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Partially differentiating both sides with respect to x:
Explore IMPLICIT Differentiation & Function Theorem Calculus 3
Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. Perform implicit differentiation of a function of two or more variables. So, if you can do calculus i derivatives you shouldn’t have too much. Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. Now let's try implicit differentiation:
Implicit Differentiation (w/ Examples And Worksheets!)
Partially differentiating both sides with respect to x: $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}. There are some situations when we have an equation implicitly defining a surface (meaning. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. So, if you can do calculus i derivatives you shouldn’t have too much.
Partial Derivatives and Implicit differentiation 1
So, if you can do calculus i derivatives you shouldn’t have too much. Now let's try implicit differentiation: Perform implicit differentiation of a function of two or more variables. Z are related implicitly if they depend on each other by an equation of the. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}.
Implicit Differentiation (w/ Examples And Worksheets!)
Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. So, if you can do calculus i derivatives you shouldn’t have too much. Z are related implicitly if they depend on each other by an equation of the. There are some situations when we have an equation implicitly defining a surface (meaning. Partial derivatives if f(x,y) is.
Perform Implicit Differentiation Of A Function Of Two Or More Variables.
There are some situations when we have an equation implicitly defining a surface (meaning. So, if you can do calculus i derivatives you shouldn’t have too much. Partial derivatives if f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as. $$ $$ 2x y^4 + x^2 4y^3 \frac{dy}{dx}.
Now Let's Try Implicit Differentiation:
Partially differentiating both sides with respect to x: Fortunately, the concept of implicit differentiation for derivatives of single variable functions can. Z are related implicitly if they depend on each other by an equation of the.