How To Find The Differential - In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. There is a natural extension to functions of three or more variables. When we first looked at derivatives, we used the leibniz. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). Draw a graph that illustrates the use of differentials to approximate the change in a quantity. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. Calculate the relative error and percentage error in using a differential. In this kind of problem we’re being asked to compute the differential of the function.
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. In this kind of problem we’re being asked to compute the differential of the function. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). Draw a graph that illustrates the use of differentials to approximate the change in a quantity. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. There is a natural extension to functions of three or more variables. In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] When we first looked at derivatives, we used the leibniz. Calculate the relative error and percentage error in using a differential.
In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. Calculate the relative error and percentage error in using a differential. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. In this kind of problem we’re being asked to compute the differential of the function. When we first looked at derivatives, we used the leibniz. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] Draw a graph that illustrates the use of differentials to approximate the change in a quantity. There is a natural extension to functions of three or more variables.
Differential Equations (Definition, Types, Order, Degree, Examples)
There is a natural extension to functions of three or more variables. Calculate the relative error and percentage error in using a differential. When we first looked at derivatives, we used the leibniz. In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. Differentials provide us with a way of estimating the.
[Solved] Find the general solution of the following differential
The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] When we first looked at derivatives, we used the leibniz. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. There is a natural extension to functions of three or more variables. In this kind of problem.
Differential Equation Calculator Examples, Facts
When we first looked at derivatives, we used the leibniz. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] There is a natural extension to functions of three or more variables. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). In other words, \(dy\) for the first problem, \(dw\) for.
Application of Differential Equation
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. In this kind of problem we’re being asked to compute the differential of the function. In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. Differentials provide us with a way of estimating.
Particular Solution of NonHomogeneous Differential Equations Mr
In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. There is a natural extension to functions of three or more variables. The differential of \(y\), denoted \(dy\), is.
coordinate systems How is Cartesian differential equation converted
In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. In this kind of problem we’re being asked to compute the differential of the function. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. The differential of \(x\),.
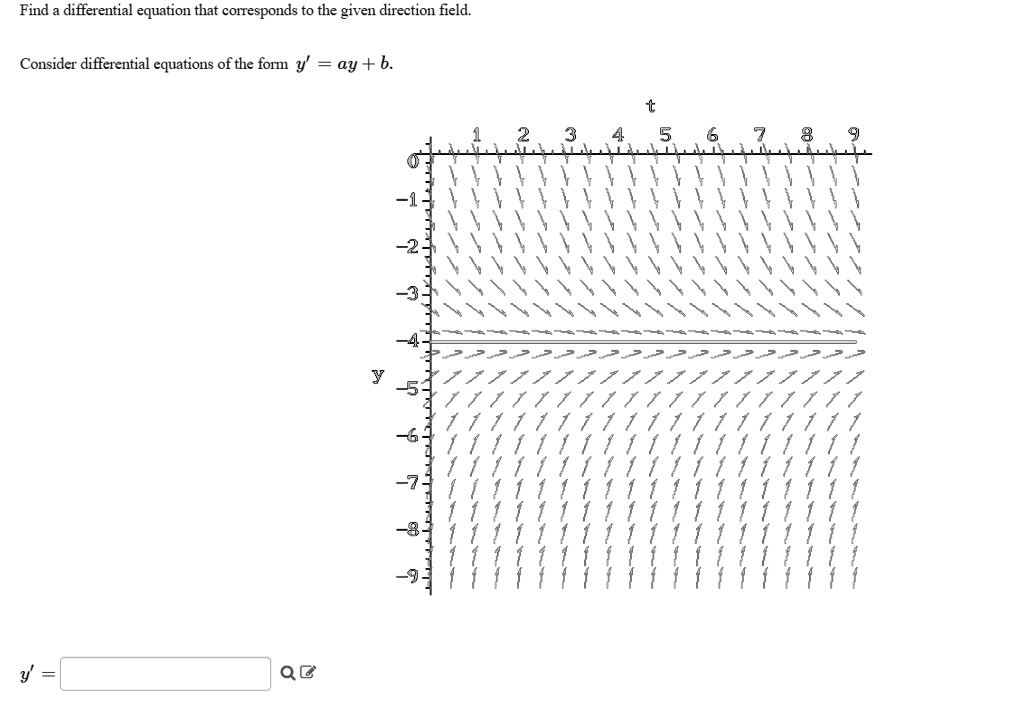
find differential equation that corresponds to the given direction
There is a natural extension to functions of three or more variables. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). Draw a graph that illustrates the use of differentials to approximate the change in a quantity. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] For instance, given the.
Android İndirme için Find Differential Detectives APK
When we first looked at derivatives, we used the leibniz. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. Calculate the relative error and percentage error in using a differential. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a.
PPT DIFFERENTIAL EQUATIONS PowerPoint Presentation, free download
Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. The differential of \(x\), denoted \(dx\), is any nonzero real number (usually taken to be a small number). When we first looked at derivatives, we used the leibniz. Calculate the relative error and percentage error in using.
[Solved] solve the partial differential equation by finding the
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. The differential of \(y\), denoted \(dy\), is \[dy = f'(x)dx.\] Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. In other words, \(dy\) for the first problem,.
The Differential Of \(Y\), Denoted \(Dy\), Is \[Dy = F'(X)Dx.\]
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx +. There is a natural extension to functions of three or more variables. In other words, \(dy\) for the first problem, \(dw\) for the second problem and \(df\) for the third. Draw a graph that illustrates the use of differentials to approximate the change in a quantity.
The Differential Of \(X\), Denoted \(Dx\), Is Any Nonzero Real Number (Usually Taken To Be A Small Number).
Calculate the relative error and percentage error in using a differential. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values. In this kind of problem we’re being asked to compute the differential of the function. When we first looked at derivatives, we used the leibniz.