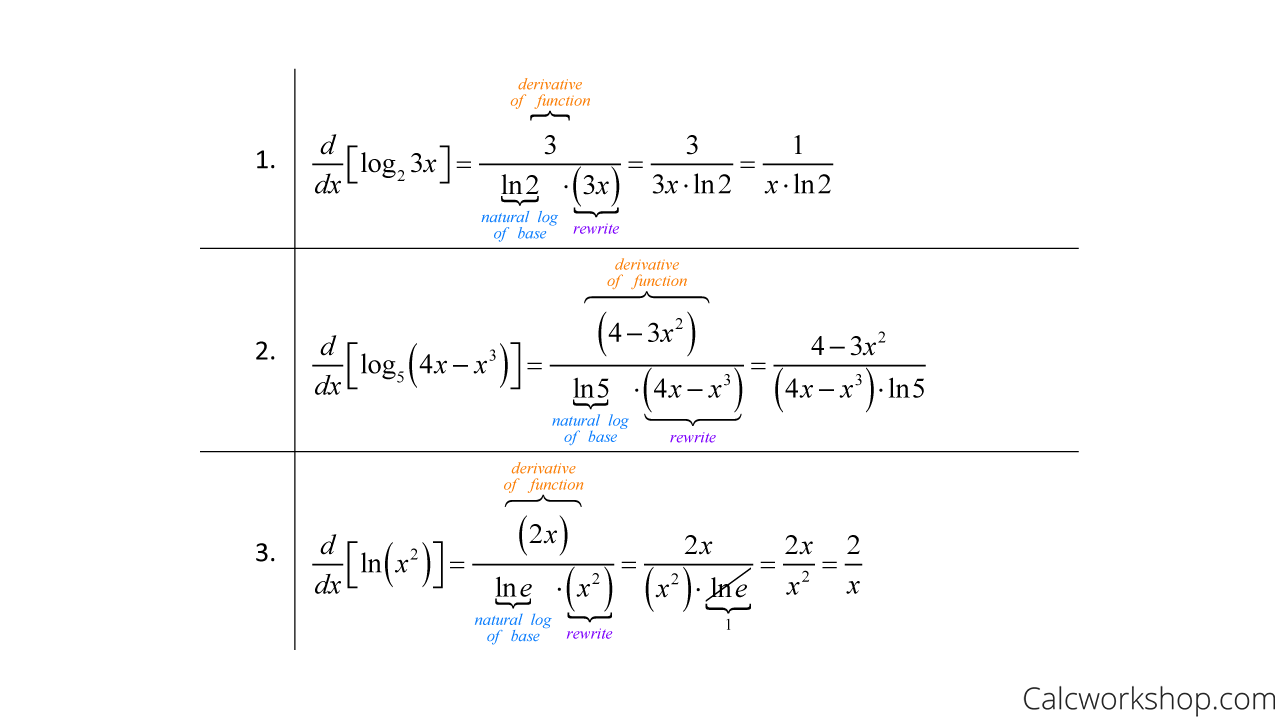
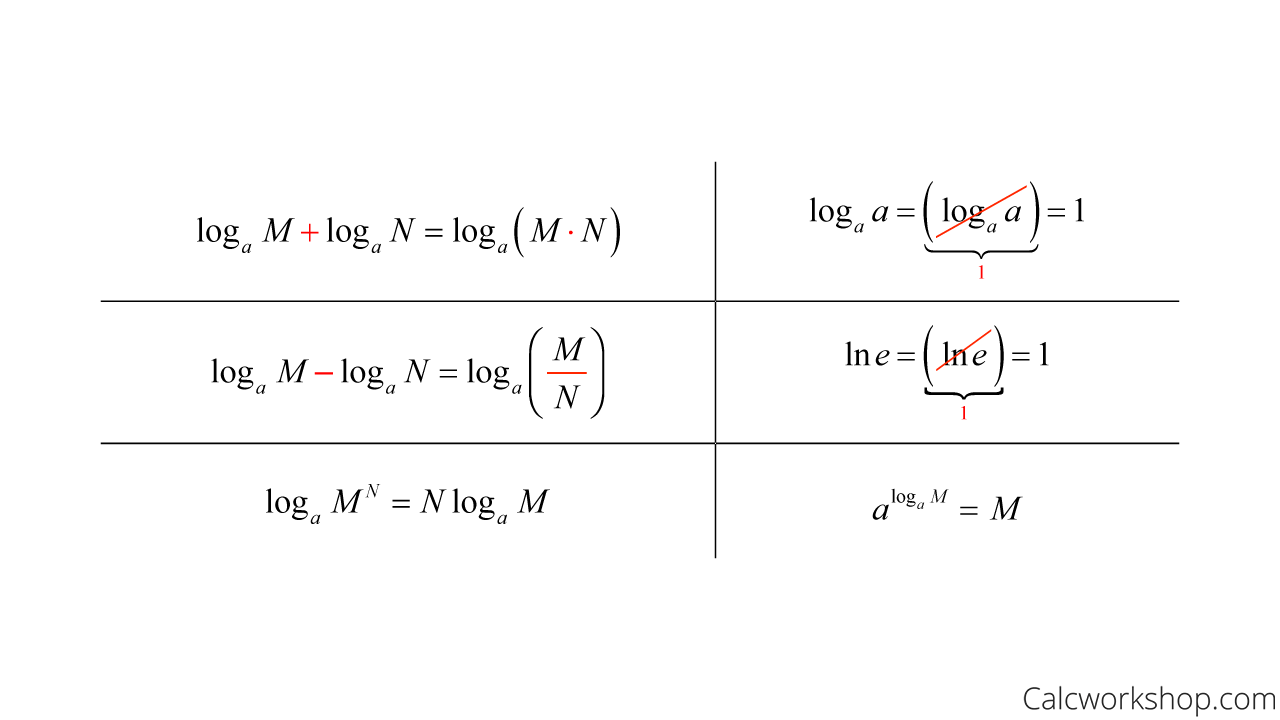
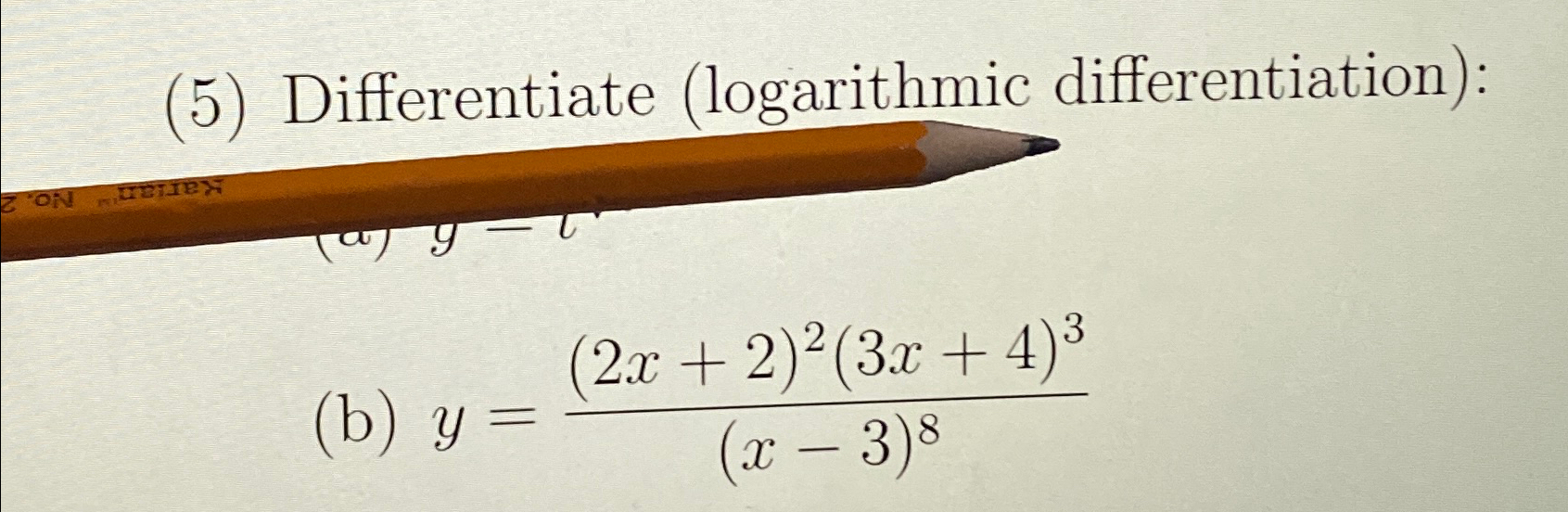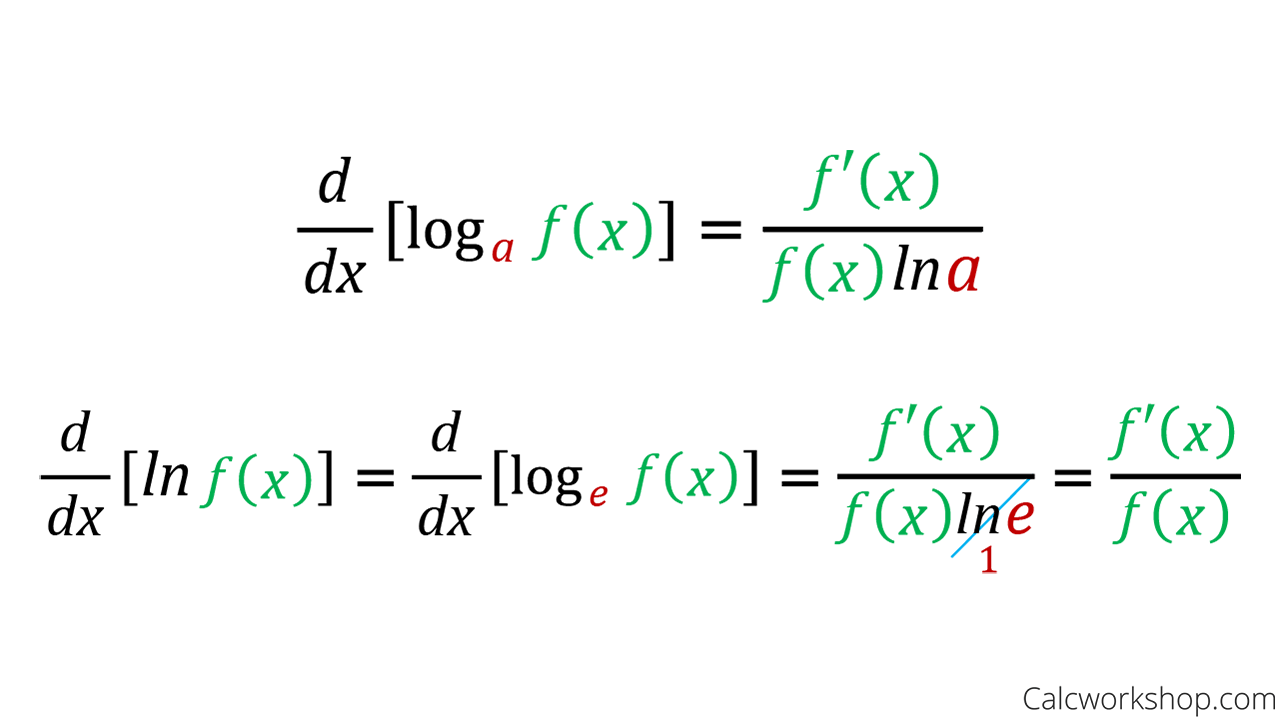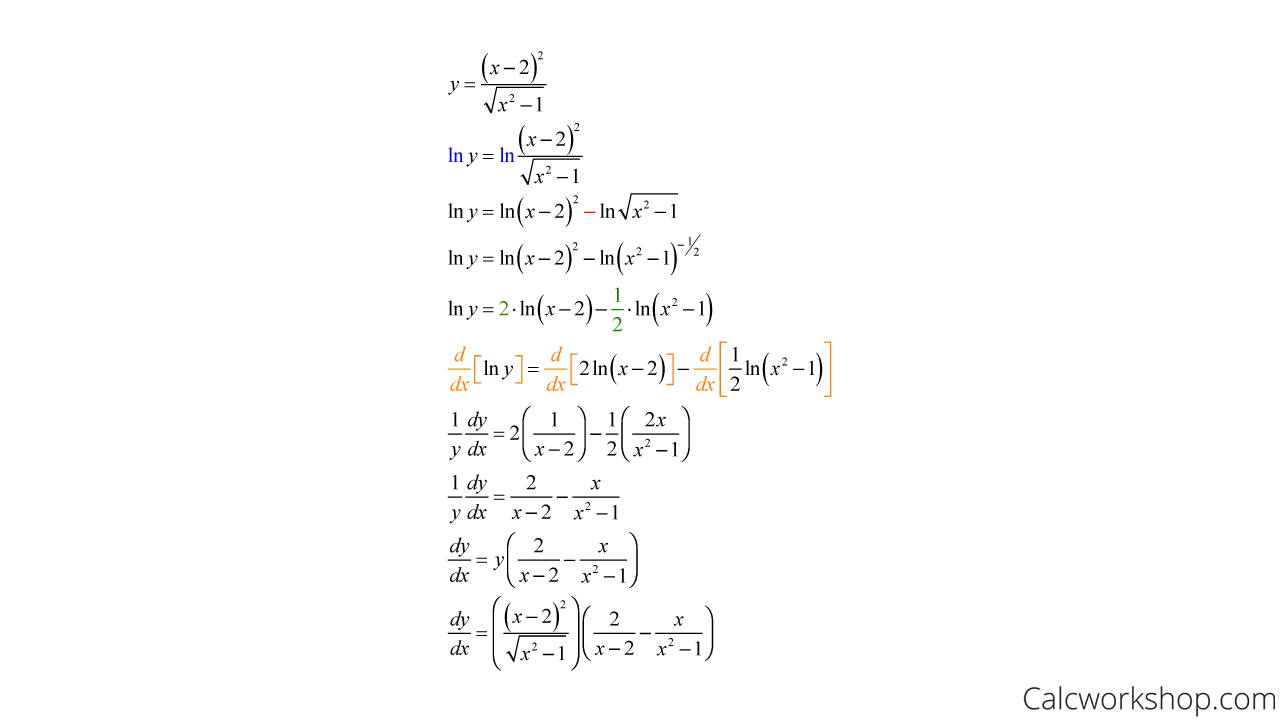How To Differentiate Logarithmic Functions - Find $$f'(x)$$ by first expanding the function and then differentiating. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. We can also use logarithmic differentiation to differentiate functions in the form. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of.
Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Find $$f'(x)$$ by first expanding the function and then differentiating. We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by.
We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Find $$f'(x)$$ by first expanding the function and then differentiating.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
Find $$f'(x)$$ by first expanding the function and then differentiating. We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. \[y = {\left(.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Find $$f'(x)$$ by first expanding the function and then differentiating.
Solved (5) Differentiate (logarithmic
Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. We can also use logarithmic differentiation to differentiate functions in.
Differentiation of Logarithmic Functions AlvinexReed
Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. We can also use logarithmic differentiation to differentiate functions in the form. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Find $$f'(x)$$ by first expanding the function and then differentiating. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or.
Derivatives of Logarithmic Functions (Fully Explained!)
Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. \[y = {\left( {f\left( x.
Derivatives of Logarithmic Functions
Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. We can also use logarithmic differentiation to differentiate functions in.
PPT Calculus Section 5.4 Differentiate logarithmic functions
We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Find $$f'(x)$$ by first expanding.
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. \[y = {\left( {f\left( x \right)} \right)^{g\left(. Find $$f'(x)$$ by first expanding the function and then differentiating.
Derivatives of Logarithmic Functions (Fully Explained!)
\[y = {\left( {f\left( x \right)} \right)^{g\left(. Find $$f'(x)$$ by first expanding the function and then differentiating. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by.
Derivatives of Logarithmic Functions (Fully Explained!)
We can also use logarithmic differentiation to differentiate functions in the form. Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Find $$f'(x)$$ by first expanding the function and then differentiating. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\).
\[Y = {\Left( {F\Left( X \Right)} \Right)^{G\Left(.
Logarithmic differentiation is a method used to find the derivative of complex functions, particularly those in the form of. We can also use logarithmic differentiation to differentiate functions in the form. Suppose $$\displaystyle f(x) = \ln\left(\frac{\sqrt x}{x^2 + 4}\right)$$. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by.