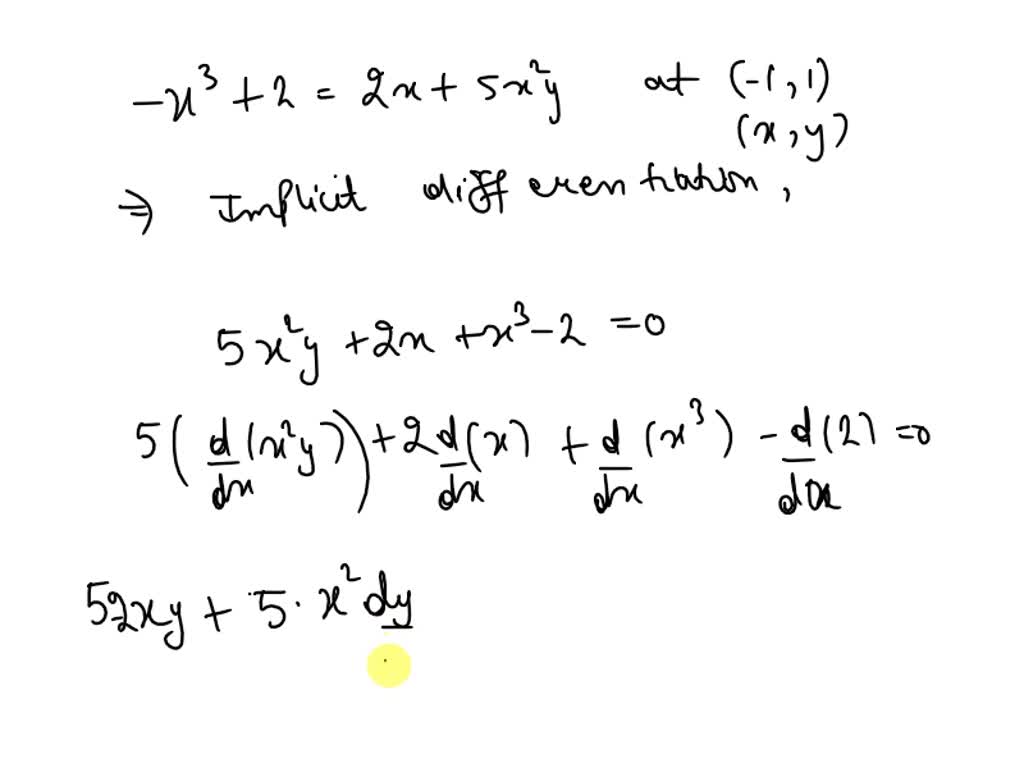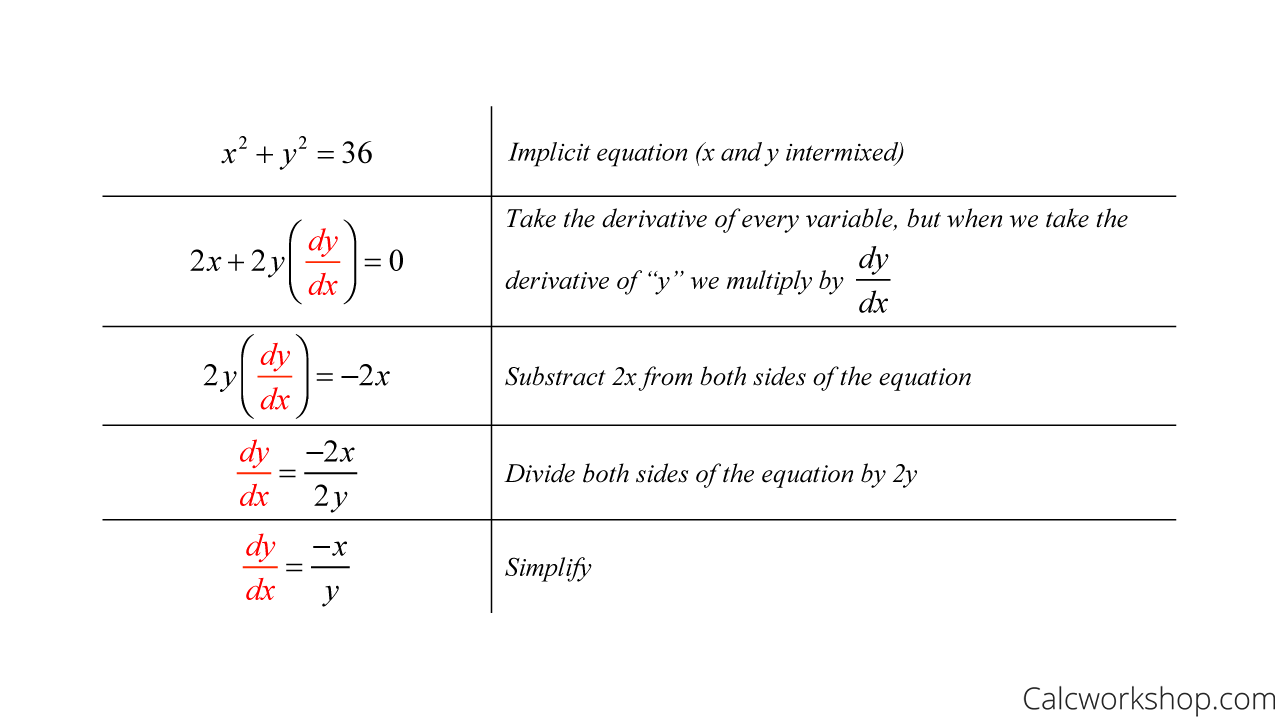How Does Implicit Differentiation Work - In this section we will discuss implicit differentiation. Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. Not every function can be explicitly written in terms of the independent. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the chain.
Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the chain. Not every function can be explicitly written in terms of the independent. In this section we will discuss implicit differentiation.
In this section we will discuss implicit differentiation. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the chain. Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. Not every function can be explicitly written in terms of the independent.
SOLVEDImplicit Differentiation Explain when you have to use implicit
In this section we will discuss implicit differentiation. Not every function can be explicitly written in terms of the independent. Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function.
intro to Implicit differentiation PDF Free Download
In this section we will discuss implicit differentiation. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the chain. Not every function can be explicitly written in terms of the independent. Implicit differentiation is a technique based on the chain rule that is.
Second Derivative Implicit DifferentiationDefinition and Properties
Not every function can be explicitly written in terms of the independent. In this section we will discuss implicit differentiation. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the chain. Implicit differentiation is a technique based on the chain rule that is.
Examples using Implicit Differentiation (solutions, formulas, videos)
Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. Not every function can be explicitly written in terms of the independent. In this section we will discuss implicit differentiation. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function.
calculus Implicit differentiation. Confusing assumption
Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. Not every function can be explicitly written in terms of the independent. In this section we will discuss implicit differentiation. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function.
Implicit Differentiation PDF Mathematical Analysis Differential
To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the chain. In this section we will discuss implicit differentiation. Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. Not every function.
PPT Implicit Differentiation PowerPoint Presentation, free download
To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the chain. Not every function can be explicitly written in terms of the independent. In this section we will discuss implicit differentiation. Implicit differentiation is a technique based on the chain rule that is.
SOLVED Implicit differentiation examples
Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. Not every function can be explicitly written in terms of the independent. In this section we will discuss implicit differentiation. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function.
How to Do Implicit Differentiation 7 Steps (with Pictures)
Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. Not every function can be explicitly written in terms of the independent. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the.
Implicit Differentiation (w/ Examples And Worksheets!)
Not every function can be explicitly written in terms of the independent. In this section we will discuss implicit differentiation. Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function.
In This Section We Will Discuss Implicit Differentiation.
Not every function can be explicitly written in terms of the independent. Implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between. To do so, take \(\ddx\) of both sides of the equation, then assume that \(y\) really is a function of \(x\) so that you can use the chain.