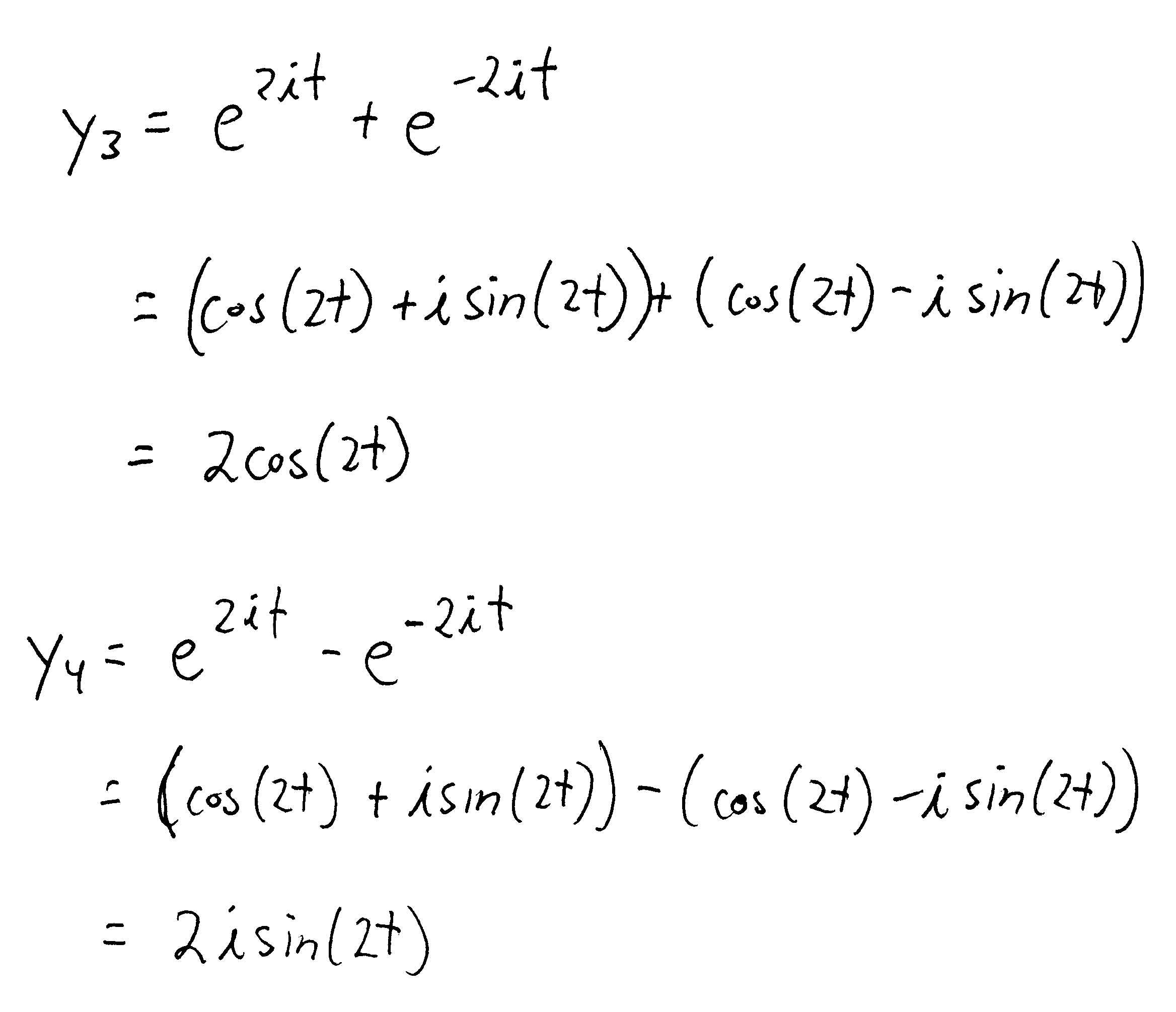Homogeneous Differential Equation Second Order - A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: The general solution of a homogeneous linear second order equation. In this tutorial, we will practise solving equations of the form: Second order (the highest derivative is of. If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. A linear nonhomogeneous differential equation of second order is represented by; A d2y dx2 +b dy dx +cy = 0. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second.
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: A d2y dx2 +b dy dx +cy = 0. The general solution of a homogeneous linear second order equation. Second order (the highest derivative is of. In this tutorial, we will practise solving equations of the form: If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. A linear nonhomogeneous differential equation of second order is represented by;
A d2y dx2 +b dy dx +cy = 0. If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. In this tutorial, we will practise solving equations of the form: A linear nonhomogeneous differential equation of second order is represented by; The general solution of a homogeneous linear second order equation. A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: Second order (the highest derivative is of.
Solved 2. Consider the following second order linear
If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. In this tutorial, we will practise solving equations of the form: A linear nonhomogeneous differential equation of second order is represented by; A d2y dx2 +b dy dx +cy = 0. The general solution of a homogeneous linear second order equation.
SOLUTION Second order homogeneous linear differential equation Studypool
Second order (the highest derivative is of. If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: In this tutorial, we will practise solving equations of the form: The general solution of a homogeneous linear second order equation.
SOLUTION Second order homogeneous linear differential equation Studypool
Second order (the highest derivative is of. A d2y dx2 +b dy dx +cy = 0. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. A linear nonhomogeneous differential equation of second order is represented by; The general solution of a homogeneous linear second order equation.
College Park Tutors Blog Differential Equations Solving a second
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. The general solution of a homogeneous linear second order equation. A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: A linear nonhomogeneous differential equation of second order is represented by;.
Solved Other questions 1. Given a homogeneous linear second
If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. The general solution of a homogeneous linear second order equation. In this tutorial, we will practise solving equations of the form: A d2y dx2 +b.
Can the solutions to a homogeneous second order differential equation
A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: A linear nonhomogeneous differential equation of second order is represented by; We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\).
SOLUTION Second order linear homogeneous differential equation Studypool
In this tutorial, we will practise solving equations of the form: The general solution of a homogeneous linear second order equation. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. Second order (the highest derivative is of. A linear nonhomogeneous differential equation of second order is represented.
SOLUTION Second order linear homogeneous differential equation Studypool
A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. In this tutorial, we will practise solving equations of the form: Second order (the highest derivative is of. The general solution.
College Park Tutors Blog Differential Equations Solving a second
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. A linear nonhomogeneous differential equation of second order is represented by; In this tutorial, we will practise solving equations of the form: If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. The general solution.
Solved For a homogeneous second order differential equation
A d2y dx2 +b dy dx +cy = 0. Second order (the highest derivative is of. A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: In this tutorial, we will practise solving equations of the form: We define fundamental sets of solutions and discuss how they can be used to get a.
A D2Y Dx2 +B Dy Dx +Cy = 0.
If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: The general solution of a homogeneous linear second order equation. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second.
Second Order (The Highest Derivative Is Of.
In this tutorial, we will practise solving equations of the form: A linear nonhomogeneous differential equation of second order is represented by;