Gateaux Differentiable - In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. Gˆateaux derivative is a generalization of the concept of.
In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept of.
In mathematics, the fr ́echet derivative is a derivative define on banach spaces. Gˆateaux derivative is a generalization of the concept of. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0).
(PDF) Gâteaux differentiable norms in MusiełakOrlicz spaces
In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. Gˆateaux derivative is a generalization of the concept of. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) =.
(PDF) Distributional Volterra series, and analysis of sequentially
In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the fr ́echet derivative is a derivative define on banach spaces. Gˆateaux derivative is a generalization of the concept.
Gateaux Lamis Dania Delesyo
Gˆateaux derivative is a generalization of the concept of. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) =.
SOLVEDLet X be a Banach space with a Gâteaux differentiable norm. Let
In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. Gˆateaux derivative is a generalization of the concept of. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) =.
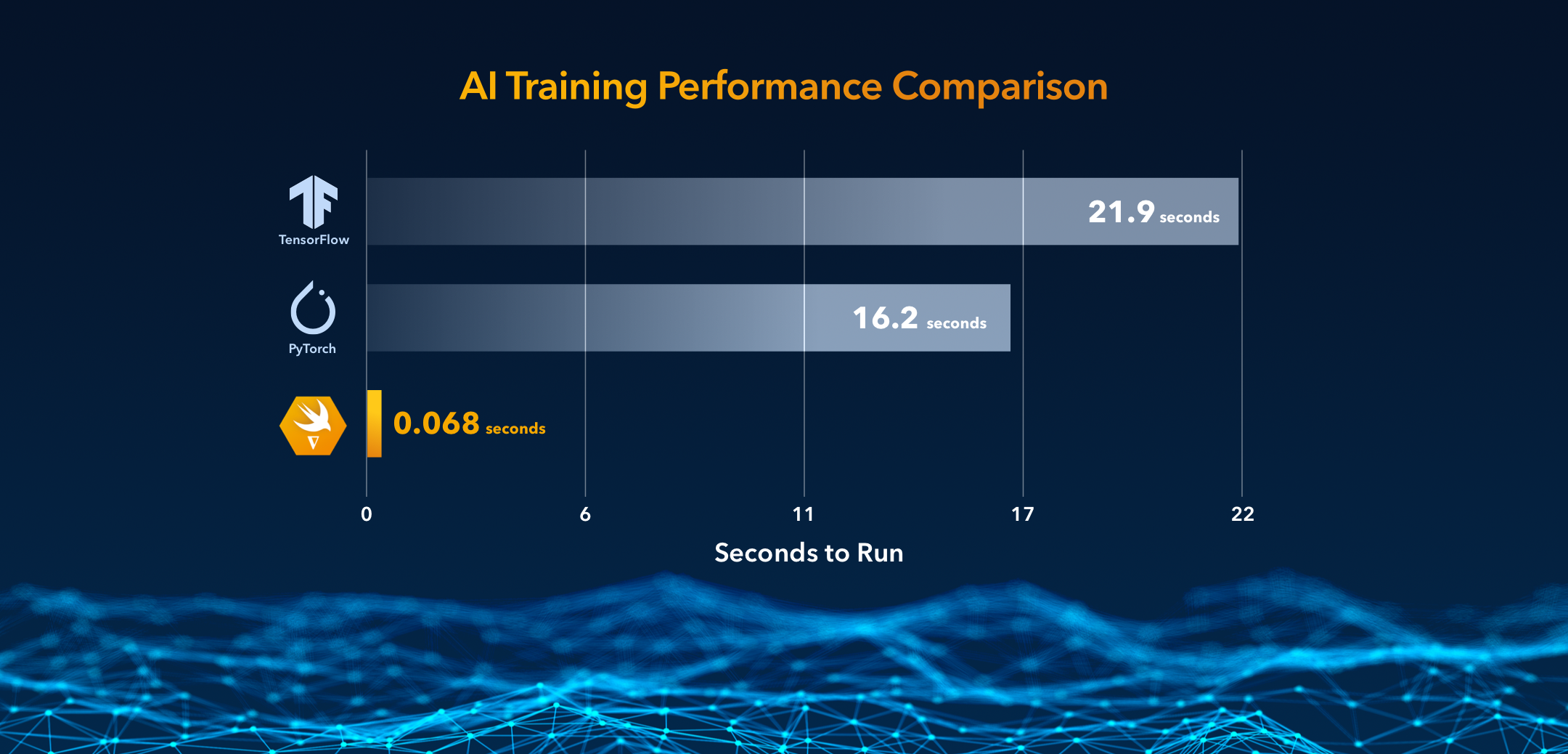
Differentiable Swift
In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. Gˆateaux derivative is a generalization of the concept of. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) =.
lesgateauxdegrandmere les recettes gourmandes des petits bonheurs
In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. Gˆateaux derivative is a generalization of the concept.
FileTypes of dessert gateaux.jpeg Wikimedia Commons
In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept of. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of.
Differentiable Font download free
Gˆateaux derivative is a generalization of the concept of. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of.
Fresh Fruit Gateaux Solstice Foods
Gˆateaux derivative is a generalization of the concept of. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of.
(PDF) Construction of pathological Gâteaux differentiable functions
If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the fr ́echet derivative is a derivative define on banach spaces. Gˆateaux derivative is a generalization of the concept of. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of.
In Mathematics, The Fr ́Echet Derivative Is A Derivative Define On Banach Spaces.
If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept of. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional.