Fundamental Matrix Differential Equations - There are many ways to pick two independent solu tions of x = a x to form the columns of φ. The fundamental matrix φ(t,t0) is a mapping of the initial condition a to the solution vector x(t). This section is devoted to fundamental matrices for linear differential equations. Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <. As t varies, the point x(t) traces out a curve in rn. The matrix valued function \( x (t) \) is called the fundamental matrix, or the fundamental matrix solution. A fundamental matrix for (1) is any matrix ψ(t) that satisfies ψ 0 (t) = p(t)ψ(t) (2) note that (2) is a first order differential equation for an unknown. It is therefore useful to have a.
The matrix valued function \( x (t) \) is called the fundamental matrix, or the fundamental matrix solution. The fundamental matrix φ(t,t0) is a mapping of the initial condition a to the solution vector x(t). Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <. There are many ways to pick two independent solu tions of x = a x to form the columns of φ. As t varies, the point x(t) traces out a curve in rn. This section is devoted to fundamental matrices for linear differential equations. It is therefore useful to have a. A fundamental matrix for (1) is any matrix ψ(t) that satisfies ψ 0 (t) = p(t)ψ(t) (2) note that (2) is a first order differential equation for an unknown.
The fundamental matrix φ(t,t0) is a mapping of the initial condition a to the solution vector x(t). As t varies, the point x(t) traces out a curve in rn. The matrix valued function \( x (t) \) is called the fundamental matrix, or the fundamental matrix solution. This section is devoted to fundamental matrices for linear differential equations. It is therefore useful to have a. A fundamental matrix for (1) is any matrix ψ(t) that satisfies ψ 0 (t) = p(t)ψ(t) (2) note that (2) is a first order differential equation for an unknown. There are many ways to pick two independent solu tions of x = a x to form the columns of φ. Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <.
Matrix differential equation Alchetron, the free social encyclopedia
It is therefore useful to have a. A fundamental matrix for (1) is any matrix ψ(t) that satisfies ψ 0 (t) = p(t)ψ(t) (2) note that (2) is a first order differential equation for an unknown. The fundamental matrix φ(t,t0) is a mapping of the initial condition a to the solution vector x(t). The matrix valued function \( x (t).
(PDF) FourthOrder Approximation of the Fundamental Matrix of Linear
This section is devoted to fundamental matrices for linear differential equations. It is therefore useful to have a. Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <. As t varies, the point x(t) traces out a curve in rn. The matrix valued function \( x (t) \).
Solved Find a fundamental matrix for the given system of
A fundamental matrix for (1) is any matrix ψ(t) that satisfies ψ 0 (t) = p(t)ψ(t) (2) note that (2) is a first order differential equation for an unknown. It is therefore useful to have a. There are many ways to pick two independent solu tions of x = a x to form the columns of φ. This section is.
(PDF) On graph differential equations and its associated matrix
It is therefore useful to have a. As t varies, the point x(t) traces out a curve in rn. The matrix valued function \( x (t) \) is called the fundamental matrix, or the fundamental matrix solution. The fundamental matrix φ(t,t0) is a mapping of the initial condition a to the solution vector x(t). This section is devoted to fundamental.
arrays Implement solution of differential equations system using
The matrix valued function \( x (t) \) is called the fundamental matrix, or the fundamental matrix solution. It is therefore useful to have a. There are many ways to pick two independent solu tions of x = a x to form the columns of φ. A fundamental matrix for (1) is any matrix ψ(t) that satisfies ψ 0 (t).
Complex Solution and Fundamental MatrixDifferential Equations and
Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <. This section is devoted to fundamental matrices for linear differential equations. The fundamental matrix φ(t,t0) is a mapping of the initial condition a to the solution vector x(t). It is therefore useful to have a. A fundamental matrix.
Modelling Motion with Differential Equations
As t varies, the point x(t) traces out a curve in rn. This section is devoted to fundamental matrices for linear differential equations. Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <. The fundamental matrix φ(t,t0) is a mapping of the initial condition a to the solution.
Systems of Matrix Differential Equations for Surfaces
This section is devoted to fundamental matrices for linear differential equations. It is therefore useful to have a. A fundamental matrix for (1) is any matrix ψ(t) that satisfies ψ 0 (t) = p(t)ψ(t) (2) note that (2) is a first order differential equation for an unknown. Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the.
Fundamental PrinciplesDifferential Equations and Their Solutions
It is therefore useful to have a. Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <. As t varies, the point x(t) traces out a curve in rn. There are many ways to pick two independent solu tions of x = a x to form the columns.
Textbooks Differential Equations Freeup
It is therefore useful to have a. This section is devoted to fundamental matrices for linear differential equations. The matrix valued function \( x (t) \) is called the fundamental matrix, or the fundamental matrix solution. Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <. The fundamental.
The Fundamental Matrix Φ(T,T0) Is A Mapping Of The Initial Condition A To The Solution Vector X(T).
Fundamental matrix suppose that x(1)(t);:::;x(n)(t) form a fundamental set of solutions for the equation x0= p(t)x (1) on some interval <t <. This section is devoted to fundamental matrices for linear differential equations. The matrix valued function \( x (t) \) is called the fundamental matrix, or the fundamental matrix solution. As t varies, the point x(t) traces out a curve in rn.
There Are Many Ways To Pick Two Independent Solu Tions Of X = A X To Form The Columns Of Φ.
It is therefore useful to have a. A fundamental matrix for (1) is any matrix ψ(t) that satisfies ψ 0 (t) = p(t)ψ(t) (2) note that (2) is a first order differential equation for an unknown.


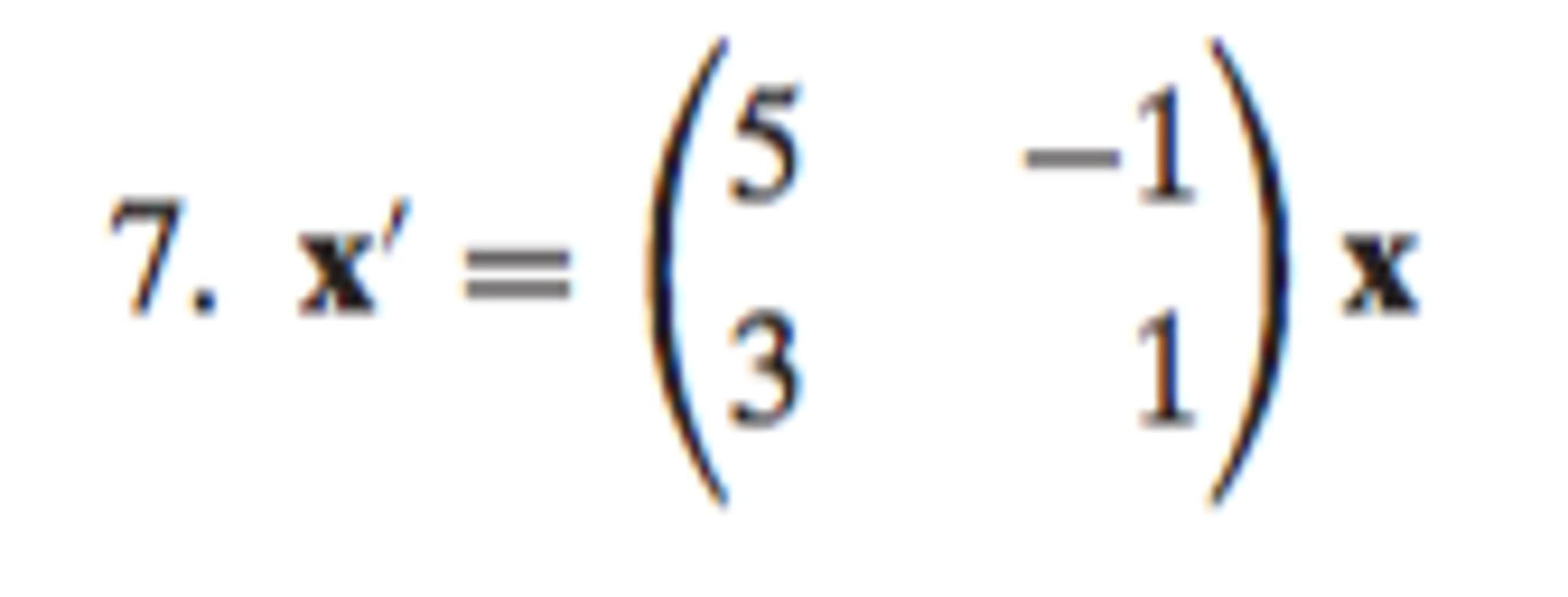






/aae14611c6e6e45b3bd99783f827f01c.jpg)