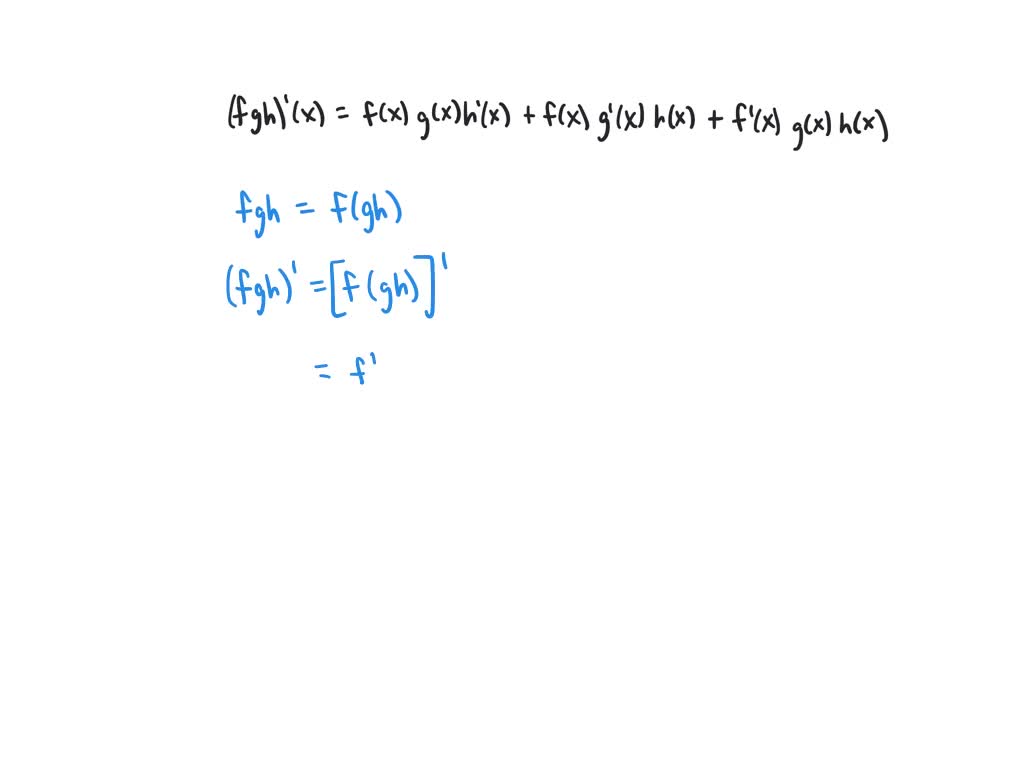Functions F G H And J Are Continuous And Differentiable - Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. The function has to be continuous. The function f, g, h and j is continuous and differentiates for all real numbers. If a function is differentiable on an. Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. H (x) = f (x) g (x) and j (x) = g (f (x)). The derivative must exist at each point in the domain of the function.
Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. The function f, g, h and j is continuous and differentiates for all real numbers. The derivative must exist at each point in the domain of the function. The function has to be continuous. H (x) = f (x) g (x) and j (x) = g (f (x)). If a function is differentiable on an. Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and.
If a function is differentiable on an. Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. The function has to be continuous. The function f, g, h and j is continuous and differentiates for all real numbers. Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. H (x) = f (x) g (x) and j (x) = g (f (x)). The derivative must exist at each point in the domain of the function.
Solved (2) Functions f.g,h, and j are continuous and
The function f, g, h and j is continuous and differentiates for all real numbers. Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. The derivative must exist at each point in the domain of the function. If a function is differentiable on an. Functions f,g,h and j are continuous and.
Solved Suppose that f and g are functions differentiable at
The function has to be continuous. H (x) = f (x) g (x) and j (x) = g (f (x)). The derivative must exist at each point in the domain of the function. Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. If a function is differentiable on an.
Solved Functions f,g,h and j are continuous and
The function has to be continuous. Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. H (x) = f (x) g (x) and j (x) = g (f (x)). If a function is differentiable on an. The function f, g, h and j is continuous and differentiates for all real numbers.
Solved If f, g, and h are differentiable functions, find
Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. The derivative must exist at each point in the domain of the function. If a function is differentiable on an. Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives.
SOLVEDLet f, g, h be differentiable functions. Show that (f g h)^'(x
H (x) = f (x) g (x) and j (x) = g (f (x)). Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. The function has to be.
Solved Functions f, g, and h continuous and differentiable
Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. H (x) = f (x) g (x) and j (x) = g (f (x)). The derivative must exist at.
[Solved] (1) Functions f, g, and h are continuous and differentiable
Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. If a function is differentiable on an. The function f, g, h and j is continuous and differentiates for all real numbers. The function has to be continuous. The derivative must exist at each point in the domain of the function.
Solved (2) Functions f, g, h, and j are continuous and
Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. H (x) = f (x) g (x) and j (x) = g (f (x)). Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and. The function has to be.
4.5 continuous functions and differentiable functions
The derivative must exist at each point in the domain of the function. Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. H (x) = f (x) g (x) and j (x) = g (f (x)). Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous.
4.5 continuous functions and differentiable functions
Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. H (x) = f (x) g (x) and j (x) = g (f (x)). The derivative must exist at each point in the domain of the function. The function has to be continuous. If a function is.
If A Function Is Differentiable On An.
H (x) = f (x) g (x) and j (x) = g (f (x)). Functions f,g,h and j are continuous and differentiable for all real numbers, and some of their values and values of their derivatives are. The derivative must exist at each point in the domain of the function. The function f, g, h and j is continuous and differentiates for all real numbers.
The Function Has To Be Continuous.
Show that if $x_0$ is in $j$, $h:j\rightarrow\mathbb{r}$ is continuous at $x_0$, $h(x)\neq h(x_0)$ if $x\neq x_0$, and.