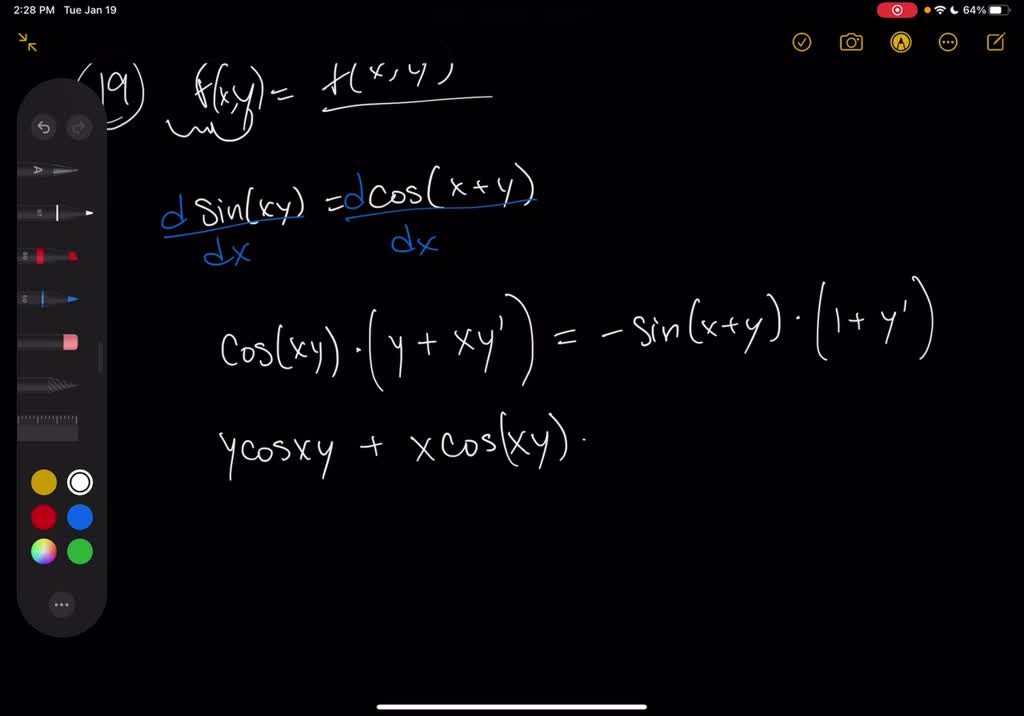
Differentiation Of Sin Xy - Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. Differentiate the right side of the equation. What is the derivative of the function y = sin(xy)? The left side would simply give you #dy/dx#. For the right side, however,. Differentiate both sides of the equation. Type in any function derivative to get the solution, steps and graph. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). You simply differentiate both sides with respect to #x#. The derivative of y y with respect to x x is y' y ′.
Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. The derivative of y y with respect to x x is y' y ′. Type in any function derivative to get the solution, steps and graph. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). Differentiate both sides of the equation. The left side would simply give you #dy/dx#. What is the derivative of the function y = sin(xy)? You simply differentiate both sides with respect to #x#. For the right side, however,. Differentiate the right side of the equation.
You simply differentiate both sides with respect to #x#. Differentiate the right side of the equation. Type in any function derivative to get the solution, steps and graph. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). The derivative of y y with respect to x x is y' y ′. What is the derivative of the function y = sin(xy)? Differentiate both sides of the equation. For the right side, however,. The left side would simply give you #dy/dx#.
[Solved] Find dy / dx by implicit differentiation. cos( xy ) = 1 + sin
Differentiate the right side of the equation. What is the derivative of the function y = sin(xy)? You simply differentiate both sides with respect to #x#. For the right side, however,. Type in any function derivative to get the solution, steps and graph.
Solved Implicit differentiation sin (x + y)^2 = (xy)^3 8
Differentiate the right side of the equation. What is the derivative of the function y = sin(xy)? Differentiate both sides of the equation. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin.
Solved If y=x+sin(xy), then
For the right side, however,. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. The derivative of y y with respect to x x is y' y ′. You simply differentiate both sides with respect to #x#. What is the derivative of the function y = sin(xy)?
Solved 1. Determine The Derivative Of X Sin^1x/ Square R...
The left side would simply give you #dy/dx#. What is the derivative of the function y = sin(xy)? Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. Differentiate both sides of the equation. Differentiate the right side of the equation.
How do you differentiate y=sin(xy)? Socratic
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). What is the derivative of the function y = sin(xy)? The left side would simply give you #dy/dx#. The derivative of y.
Solved Use implicit differentiation to find dy/dx. Cos xy +
You simply differentiate both sides with respect to #x#. The derivative of y y with respect to x x is y' y ′. Differentiate the right side of the equation. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f.
Solved For Sin (XY) X = 0 Using Implicit Differentiatio...
Type in any function derivative to get the solution, steps and graph. Differentiate the right side of the equation. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where.
Solved Find dy/dx by implicit differentiation. cos (xy)=sin (x+y) dy
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x). Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. Differentiate the right side of the equation. The derivative of.
Find dy/dx by implicit differentiation. sin(xy) = cos(x+y) Numerade
Differentiate the right side of the equation. Type in any function derivative to get the solution, steps and graph. The derivative of y y with respect to x x is y' y ′. What is the derivative of the function y = sin(xy)? Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g.
[Solved] . sin xy = x 2 + y. y Cos xy = X lue in the red box is lue
For the right side, however,. What is the derivative of the function y = sin(xy)? Differentiate both sides of the equation. The derivative of y y with respect to x x is y' y ′. You simply differentiate both sides with respect to #x#.
Differentiate The Right Side Of The Equation.
Differentiate both sides of the equation. Type in any function derivative to get the solution, steps and graph. Dy dx = ycos(xy) 1 −xcos(xy) using implicit differentiation, the product rule,. What is the derivative of the function y = sin(xy)?
The Left Side Would Simply Give You #Dy/Dx#.
The derivative of y y with respect to x x is y' y ′. You simply differentiate both sides with respect to #x#. For the right side, however,. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = sin(x) f (x) = sin (x).
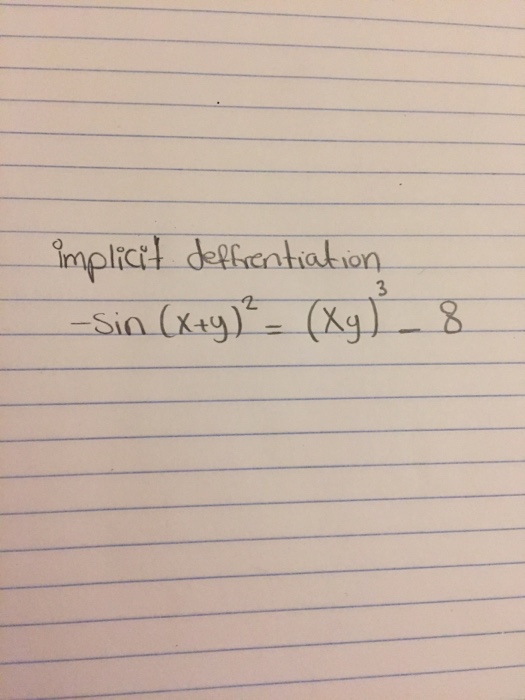
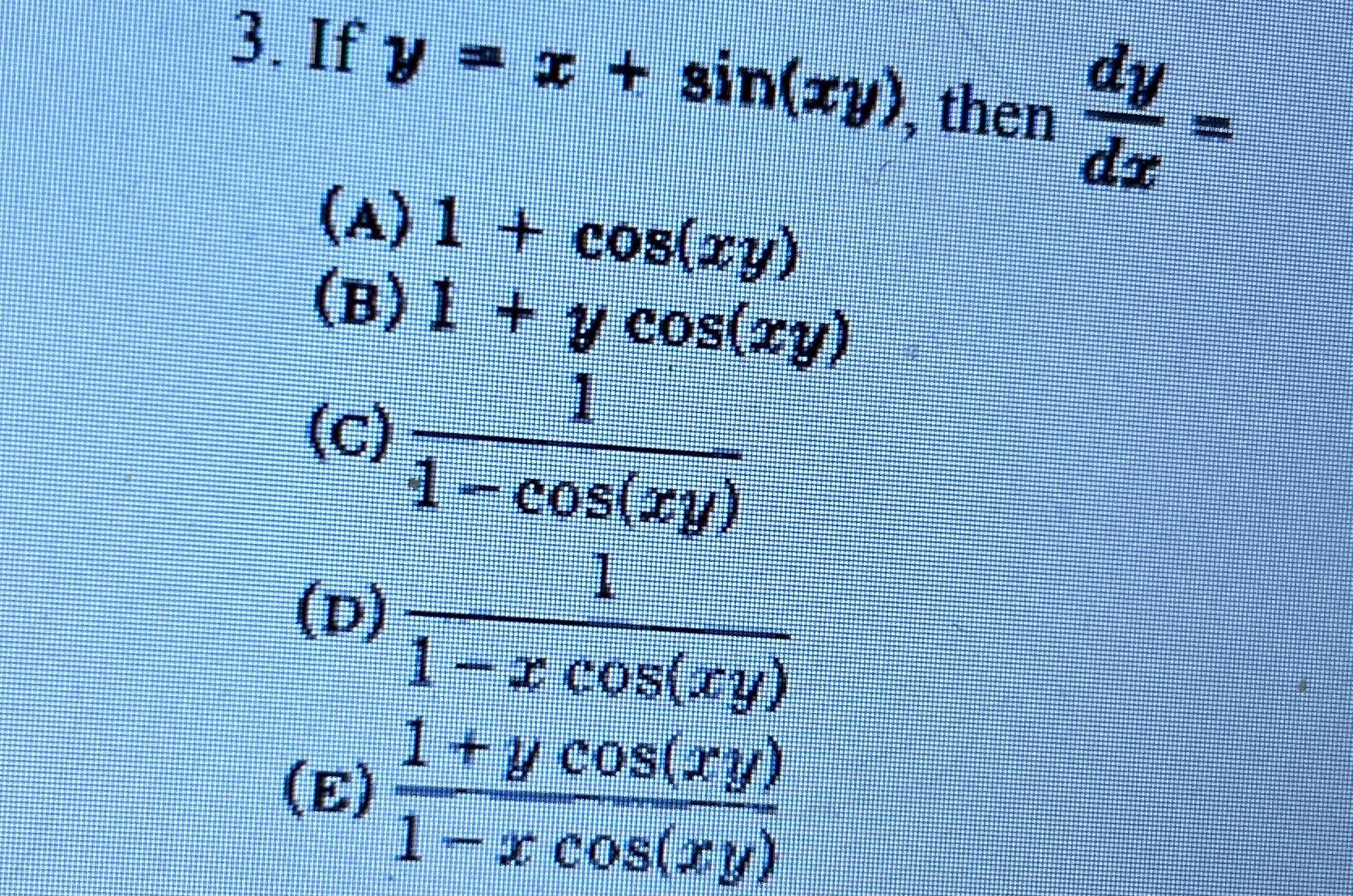

.png)