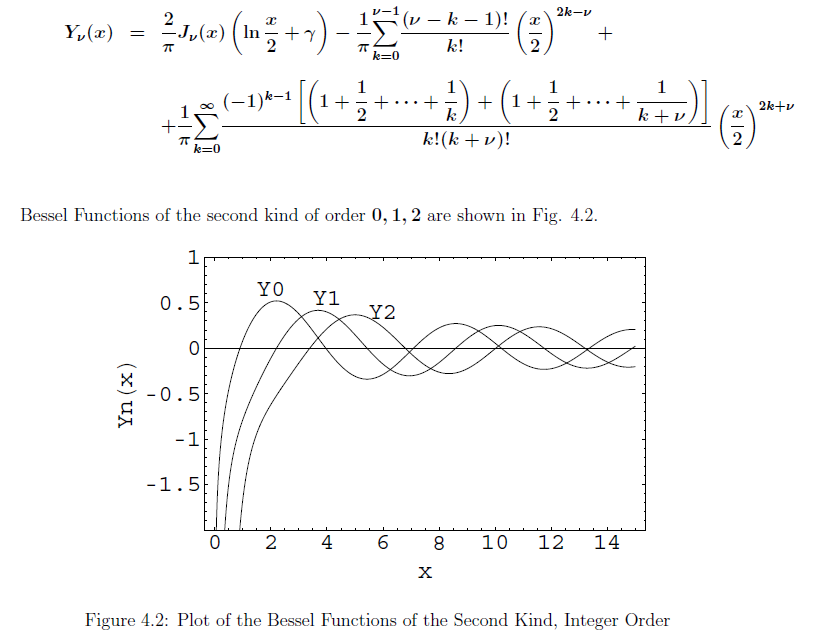
Differentiation Of Bessel Function - Let’s begin with a derivative. Integrating the differential relations leads to the integral relations. There are numerous identities involving bessel functions which may now be generated using the above definitions. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series.
We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Let’s begin with a derivative. There are numerous identities involving bessel functions which may now be generated using the above definitions. Integrating the differential relations leads to the integral relations.
Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Integrating the differential relations leads to the integral relations. Let’s begin with a derivative. There are numerous identities involving bessel functions which may now be generated using the above definitions. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation.
Modified Bessel Function Table
We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Let’s begin with a derivative. There are numerous identities involving bessel functions which may now be.
Bessel Function Of Second Kind Skedbooks
Let’s begin with a derivative. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. There are numerous identities involving bessel functions which may now be generated using the above definitions. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x.
Zeroth‐order Bessel function of the first kind. Download Scientific
There are numerous identities involving bessel functions which may now be generated using the above definitions. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series..
Generating Function For Bessel Function
Let’s begin with a derivative. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. There are numerous identities involving bessel functions which may now be generated using the above definitions. Integrating the differential relations leads to the integral relations. We begin with a derivation of the.
(PDF) A differentiation formula for spherical Bessel functions
Let’s begin with a derivative. There are numerous identities involving bessel functions which may now be generated using the above definitions. Integrating the differential relations leads to the integral relations. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. We begin with a derivation of the.
integration product of bessel function integral Mathematics Stack
There are numerous identities involving bessel functions which may now be generated using the above definitions. Integrating the differential relations leads to the integral relations. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. We begin with a derivation of the bessel functions ja(x) and ya(x),.
Properties Of Bessel Function Skedbooks
We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. There are numerous identities involving bessel functions which may now be generated using the above definitions..
integration product of bessel function integral Mathematics Stack
Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. There are numerous identities involving bessel functions which may now be generated using the above definitions..
Bessel Function Series Solution
Integrating the differential relations leads to the integral relations. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Let’s begin with a derivative. There are.
Generating Function For Bessel Function
Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Let’s begin with a derivative. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. There are numerous identities involving bessel functions which may now be.
Integrating The Differential Relations Leads To The Integral Relations.
We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Let’s begin with a derivative. There are numerous identities involving bessel functions which may now be generated using the above definitions. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series.