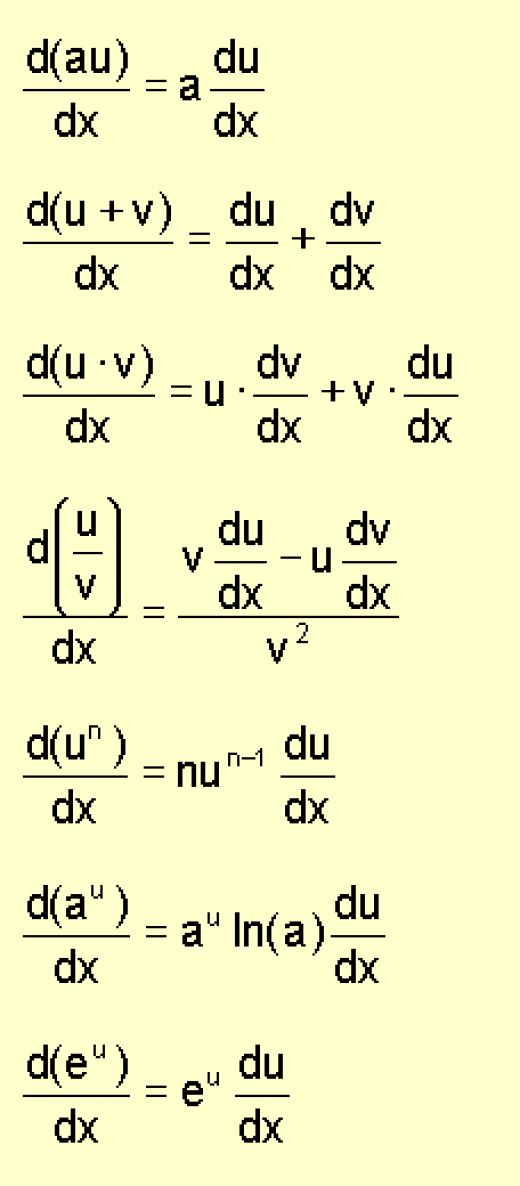Differentiation Of A Definite Integral - Under fairly loose conditions on the. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. Derivative of a definite integral. For an integral of the. For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. The derivative of a definite integral refers to finding the rate of change of the integral with respect.
Under fairly loose conditions on the. For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. For an integral of the. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. The derivative of a definite integral refers to finding the rate of change of the integral with respect. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. Derivative of a definite integral.
Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. Under fairly loose conditions on the. The derivative of a definite integral refers to finding the rate of change of the integral with respect. Derivative of a definite integral. For an integral of the.
Definite Integral Formula Learn Formula to Calculate Definite Integral
For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. Under fairly loose conditions on the. The derivative of a definite integral refers to finding the rate of change of the integral with respect. For an integral of the. Unless the variable x appears in either (or both) of the limits of integration,.
PPT 4010Properties of the Definite Integral (5.3) PowerPoint
Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. For an integral of the. The derivative of a definite integral refers to finding the rate of change of the integral with respect. Derivative of a definite integral. For a definite integral.
SOLUTION Differentiation under integral sign Studypool
For an integral of the. The derivative of a definite integral refers to finding the rate of change of the integral with respect. Derivative of a definite integral. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. Differentiation under the integral.
Maths Tips and Tricks INDEFINITE INTEGRAL , DIFFERENTIATION , DEFINITE
Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Under fairly loose conditions on the. For an integral of the. The derivative of a definite integral refers to finding the rate of change of the integral with respect. Unless the variable x appears in either (or both) of the limits of integration, the result.
Integral Wikipedia
Under fairly loose conditions on the. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. The derivative of a definite integral refers to finding.
Maths Tips and Tricks INDEFINITE INTEGRAL , DIFFERENTIATION , DEFINITE
For an integral of the. For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. Under fairly loose conditions on the. Derivative of a definite integral. The derivative of a definite integral refers to finding the rate of change of the integral with respect.
The Definite Integral The Definite Integral What is the Definite
For an integral of the. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. The derivative of a definite integral refers to finding the rate of change of the integral with respect. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not.
Maths Tips and Tricks INDEFINITE INTEGRAL , DIFFERENTIATION , DEFINITE
Derivative of a definite integral. For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. For an integral of the. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Under fairly loose conditions on the.
Maths Tips and Tricks INDEFINITE INTEGRAL , DIFFERENTIATION , DEFINITE
The derivative of a definite integral refers to finding the rate of change of the integral with respect. For an integral of the. For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. Derivative of a definite integral. Under fairly loose conditions on the.
Maths Tips and Tricks INDEFINITE INTEGRAL , DIFFERENTIATION , DEFINITE
For a definite integral with a variable upper limit of integration $\int_a^xf(t)\,dt$, you have ${d\over dx} \int_a^xf(t)\,dt=f(x)$. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Derivative of a definite integral. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve.
For A Definite Integral With A Variable Upper Limit Of Integration $\Int_A^xf(T)\,Dt$, You Have ${D\Over Dx} \Int_A^xf(T)\,Dt=F(X)$.
Derivative of a definite integral. The derivative of a definite integral refers to finding the rate of change of the integral with respect. Under fairly loose conditions on the. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals.
For An Integral Of The.
Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative.