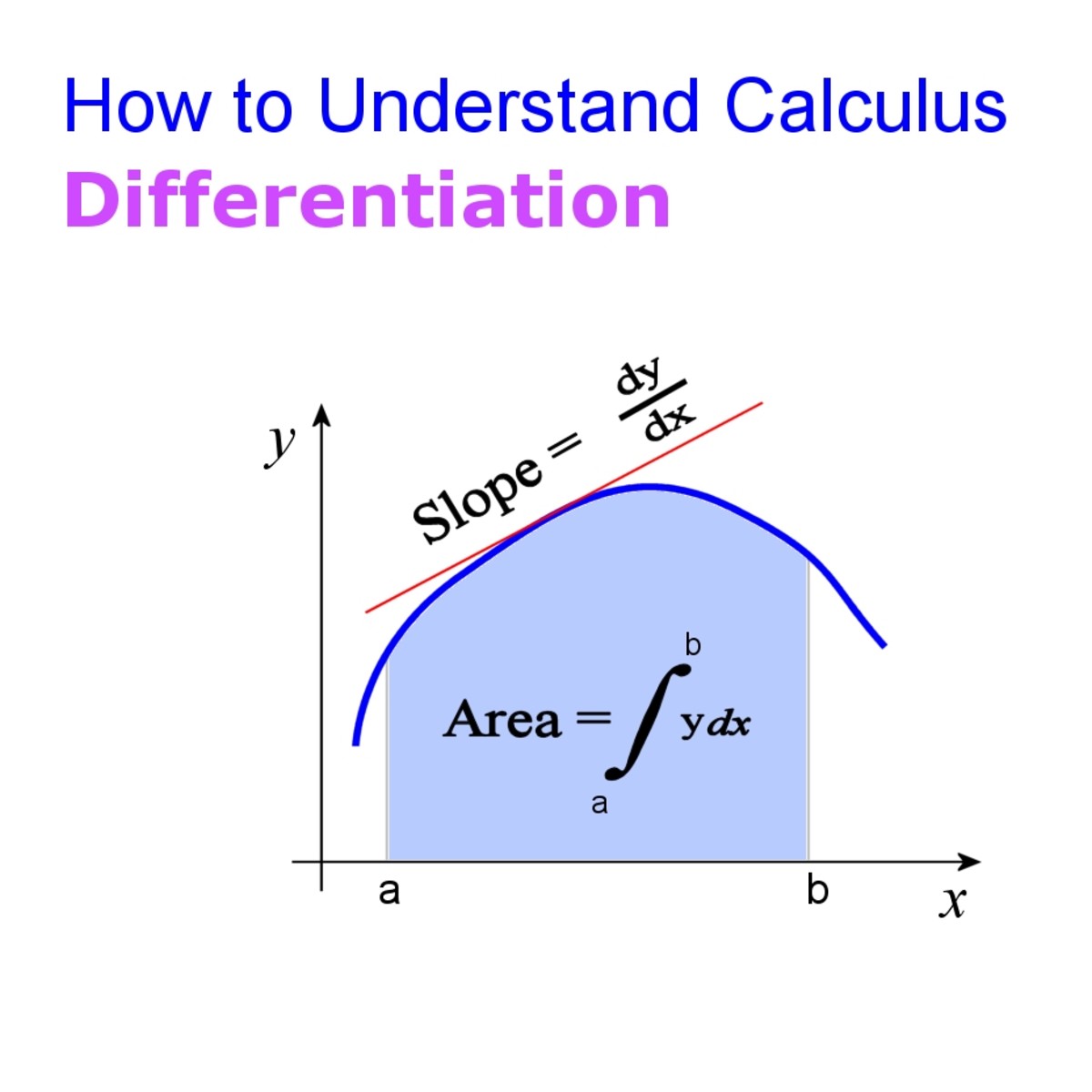
Differentiation Limits - What role do limits play in determining whether or not a function is continuous at a point? The rate at which f. Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at x, i.e. The concepts of limits, continuity, and differentiability is essential in calculus and its applications. Limits provide a way to analyze. Is differentiable at x = a?.
The rate at which f. Limits provide a way to analyze. Is differentiable at x = a?. What role do limits play in determining whether or not a function is continuous at a point? The concepts of limits, continuity, and differentiability is essential in calculus and its applications. Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at x, i.e.
For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at x, i.e. Is differentiable at x = a?. Limits provide a way to analyze. What role do limits play in determining whether or not a function is continuous at a point? The concepts of limits, continuity, and differentiability is essential in calculus and its applications. The rate at which f. Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point.
Differentiation Formula Limits at Jane blog
Limits provide a way to analyze. The concepts of limits, continuity, and differentiability is essential in calculus and its applications. For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at x, i.e. Is differentiable at x = a?. The rate at which f.
SOLUTION Chapter 1 Differentiation & Limits Presentation Studypool
Limits provide a way to analyze. Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. Is differentiable at x = a?. For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at x, i.e. The rate at which f.
RHS AP Calc BC 201011 Limits, Continuity, Differentiation
What role do limits play in determining whether or not a function is continuous at a point? The concepts of limits, continuity, and differentiability is essential in calculus and its applications. Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. Limits provide a way to analyze. Is differentiable at.
Differentiation Rules and Limits Review Task Cards Calclus Google
The concepts of limits, continuity, and differentiability is essential in calculus and its applications. What role do limits play in determining whether or not a function is continuous at a point? Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. For a general function f(x), the derivative f′(x) represents.
Limits and Differentiation. jmwteacher Free Programs and Videos
Limits provide a way to analyze. Is differentiable at x = a?. For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at x, i.e. The rate at which f. Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point.
Differentiation Formula Limits at Jane blog
What role do limits play in determining whether or not a function is continuous at a point? Is differentiable at x = a?. Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. The concepts of limits, continuity, and differentiability is essential in calculus and its applications. The rate at.
Limits and Differentiation from First Principles Mathematics and
Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at x, i.e. The rate at which f. Limits provide a way to analyze. Is differentiable at x = a?.
SOLUTION Limits and differentiation formulae Studypool
Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. What role do limits play in determining whether or not a function is continuous at a point? The concepts of limits, continuity, and differentiability is essential in calculus and its applications. The rate at which f. Limits provide a way.
Differentiation Using Limits PDF Derivative Function (Mathematics)
Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. The rate at which f. For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at x, i.e. Limits provide a way to analyze. What role do limits play in determining whether or not.
Differentiation Formula Limits at Jane blog
Limits provide a way to analyze. Limit definition of a derivative is the foundational concept in calculus for understanding how functions change at a specific point. What role do limits play in determining whether or not a function is continuous at a point? For a general function f(x), the derivative f′(x) represents the instantaneous rate of change of f at.
Limit Definition Of A Derivative Is The Foundational Concept In Calculus For Understanding How Functions Change At A Specific Point.
Limits provide a way to analyze. Is differentiable at x = a?. The rate at which f. The concepts of limits, continuity, and differentiability is essential in calculus and its applications.
For A General Function F(X), The Derivative F′(X) Represents The Instantaneous Rate Of Change Of F At X, I.e.
What role do limits play in determining whether or not a function is continuous at a point?