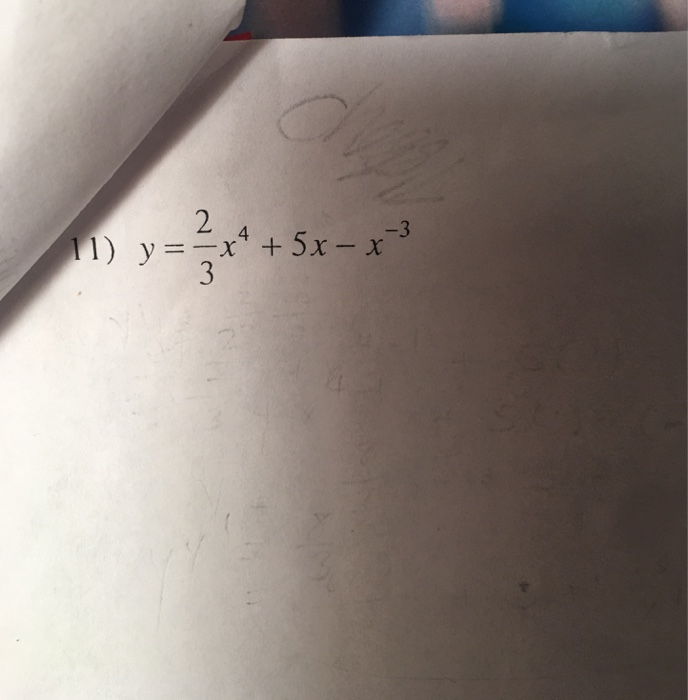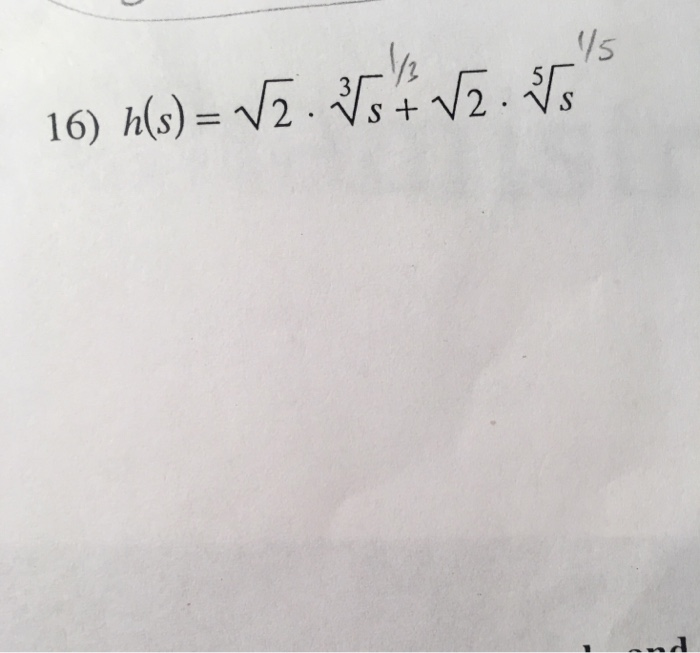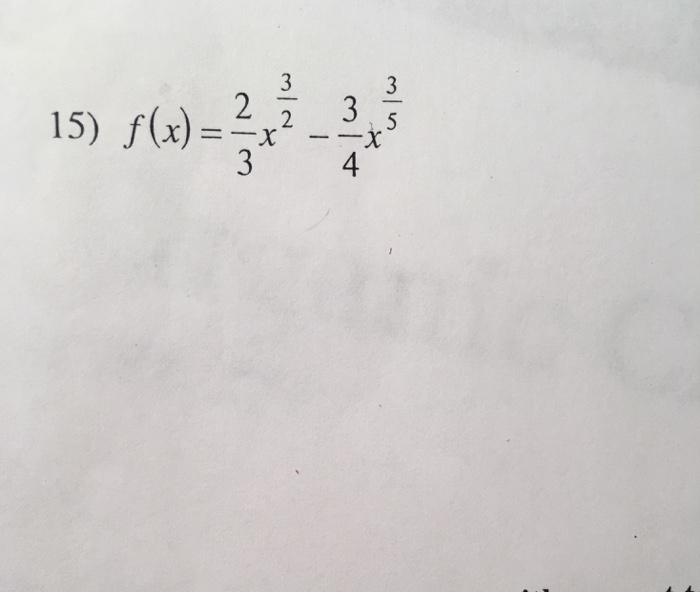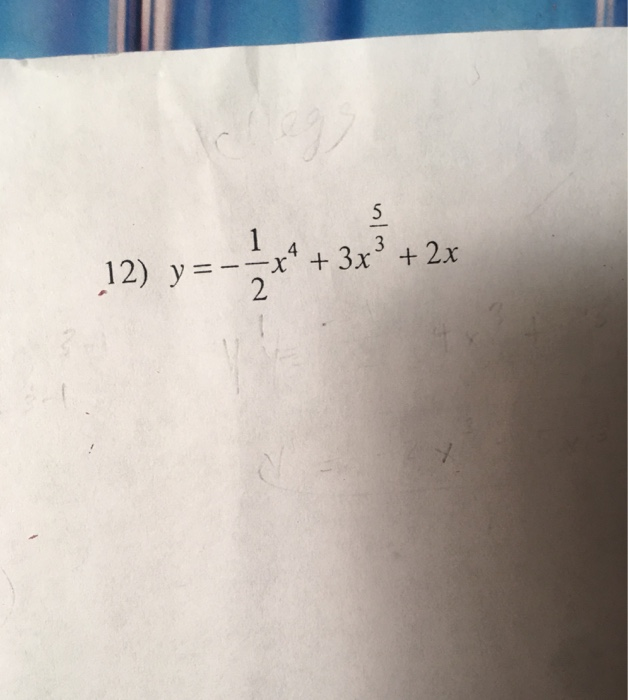Differentiate With Respect To X - To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. Key point d dx (f(y)) = d dy (f(y))× dy dx. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The derivative with respect to $x$ is:
The derivative with respect to $x$ is: To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. Key point d dx (f(y)) = d dy (f(y))× dy dx. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$.
Key point d dx (f(y)) = d dy (f(y))× dy dx. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The derivative with respect to $x$ is: The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx.
Solved Differentiate each function with respect to x.
To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The derivative with respect to $x$ is: The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. At what rate does $f$.
Solved Differentiate The Following Functions With Respect...
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation calculator will find the first and second.
Solved Differentiate each function with respect to x.
The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. Key point d dx (f(y)) = d dy (f(y))× dy dx. The.
Differentiate the following with respect to x (sin x)^x + (cos x)^sinx
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. To differentiate a function of y.
Differentiate the following function with respect to x. 2x^2 + 3x + 4x
Key point d dx (f(y)) = d dy (f(y))× dy dx. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The derivative with respect to $x$ is: The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$.
Solved Differentiate each function with respect to x.
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation calculator will find the first and second.
Ex 5.2, 8 Differentiate cos (root x) with respect to x
The derivative with respect to $x$ is: The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. At what rate does $f$.
Solved Differentiate each function with respect to x.
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. Key point d dx (f(y)) = d dy (f(y))× dy dx. To differentiate a function of y.
Differentiate with respect to x Maths Continuity and
Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The derivative with respect to $x$.
Differentiate it with respect to X using general rules Maths Limits
The derivative with respect to $x$ is: To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation.
The Derivative With Respect To $X$ Is:
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx.