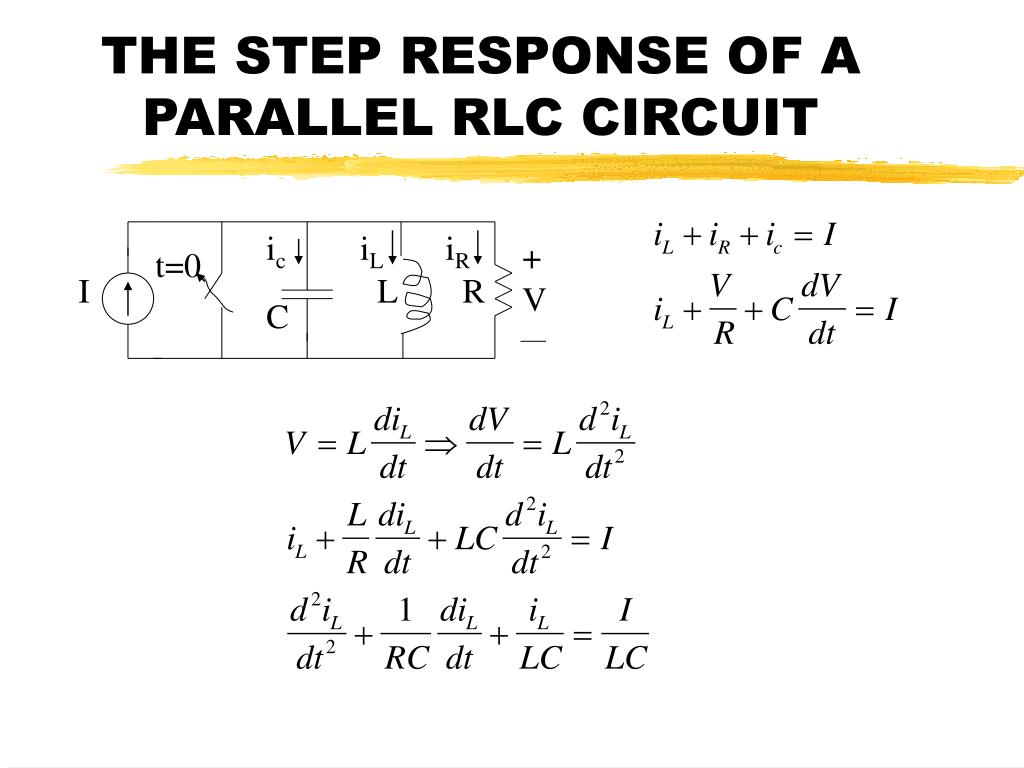
Differential Equations Rlc Circuit - Since k =constant, a particular solution is simply y(p)(t) = k=b. In the context of rlc circuits, y(p)(t). Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. In equations (2) √ and (4) the practical resonance is always at the natural.
Since k =constant, a particular solution is simply y(p)(t) = k=b. In equations (2) √ and (4) the practical resonance is always at the natural. Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. In the context of rlc circuits, y(p)(t).
Since k =constant, a particular solution is simply y(p)(t) = k=b. In the context of rlc circuits, y(p)(t). Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. In equations (2) √ and (4) the practical resonance is always at the natural.
Dc Rlc Circuit Equations Tessshebaylo
In the context of rlc circuits, y(p)(t). Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. In equations (2) √ and (4) the practical resonance is always at the natural. Since k =constant, a particular solution is simply y(p)(t) = k=b.
Rlc circuits and differential equations1 PPT
Since k =constant, a particular solution is simply y(p)(t) = k=b. Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. In the context of rlc circuits, y(p)(t). In equations (2) √ and (4) the practical resonance is always at the natural.
Rlc circuits and differential equations1 PPT
In equations (2) √ and (4) the practical resonance is always at the natural. In the context of rlc circuits, y(p)(t). Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. Since k =constant, a particular solution is simply y(p)(t) = k=b.
Rlc circuits and differential equations1 PPT
Since k =constant, a particular solution is simply y(p)(t) = k=b. Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. In the context of rlc circuits, y(p)(t). In equations (2) √ and (4) the practical resonance is always at the natural.
"RLC Circuit, Differential Equation Electrical Engineering Basics
Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. In the context of rlc circuits, y(p)(t). In equations (2) √ and (4) the practical resonance is always at the natural. Since k =constant, a particular solution is simply y(p)(t) = k=b.
Rlc circuits and differential equations1 PPT
In equations (2) √ and (4) the practical resonance is always at the natural. Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. Since k =constant, a particular solution is simply y(p)(t) = k=b. In the context of rlc circuits, y(p)(t).
Rlc circuits and differential equations1 PPT
In equations (2) √ and (4) the practical resonance is always at the natural. Since k =constant, a particular solution is simply y(p)(t) = k=b. In the context of rlc circuits, y(p)(t). Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three.
Parallel Rlc Circuit Equations Hot Sex Picture
In the context of rlc circuits, y(p)(t). Since k =constant, a particular solution is simply y(p)(t) = k=b. In equations (2) √ and (4) the practical resonance is always at the natural. Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three.
Rlc circuits and differential equations1 PPT
Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. Since k =constant, a particular solution is simply y(p)(t) = k=b. In equations (2) √ and (4) the practical resonance is always at the natural. In the context of rlc circuits, y(p)(t).
Rlc circuits and differential equations1 PPT
In the context of rlc circuits, y(p)(t). In equations (2) √ and (4) the practical resonance is always at the natural. Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three. Since k =constant, a particular solution is simply y(p)(t) = k=b.
In Equations (2) √ And (4) The Practical Resonance Is Always At The Natural.
In the context of rlc circuits, y(p)(t). Since k =constant, a particular solution is simply y(p)(t) = k=b. Figure 2 shows the response of the series rlc circuit with l=47mh, c=47nf and for three.