Differential Equations Laplace Transform - Detailed explanations and steps are also included. We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. Let us see how the laplace transform is used for differential equations. One of the typical applications of laplace transforms is the solution of nonhomogeneous linear constant coefficient differential equations. In this section we will examine how to use laplace transforms to solve ivp’s. First let us try to find the laplace transform of a function that is a derivative. The examples in this section are restricted to differential equations that could be solved. The use of laplace transforms to solve differential equations is presented along with detailed solutions. In addition, we will define the convolution integral and show.
Detailed explanations and steps are also included. Let us see how the laplace transform is used for differential equations. First let us try to find the laplace transform of a function that is a derivative. The use of laplace transforms to solve differential equations is presented along with detailed solutions. We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. In this section we will examine how to use laplace transforms to solve ivp’s. One of the typical applications of laplace transforms is the solution of nonhomogeneous linear constant coefficient differential equations. In addition, we will define the convolution integral and show. The examples in this section are restricted to differential equations that could be solved.
One of the typical applications of laplace transforms is the solution of nonhomogeneous linear constant coefficient differential equations. We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. Let us see how the laplace transform is used for differential equations. The examples in this section are restricted to differential equations that could be solved. Detailed explanations and steps are also included. In this section we will examine how to use laplace transforms to solve ivp’s. In addition, we will define the convolution integral and show. The use of laplace transforms to solve differential equations is presented along with detailed solutions. First let us try to find the laplace transform of a function that is a derivative.
[Solved] The Laplace transform of the function, whose graph is the
One of the typical applications of laplace transforms is the solution of nonhomogeneous linear constant coefficient differential equations. The examples in this section are restricted to differential equations that could be solved. In this section we will examine how to use laplace transforms to solve ivp’s. In addition, we will define the convolution integral and show. The use of laplace.
Calculating laplace transforms StudyPug
We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. The examples in this section are restricted to differential equations that could be solved. In addition, we will define the convolution integral and show. One of the typical applications of laplace transforms is the solution of nonhomogeneous linear constant coefficient differential equations. The use.
SOLUTION Solving simultaneous linear differential equations by using
We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. First let us try to find the laplace transform of a function that is a derivative. In addition, we will define the convolution integral and show. The use of laplace transforms to solve differential equations is presented along with detailed solutions. In this section.
(PDF) New perspectives of the Laplace transform in partial
One of the typical applications of laplace transforms is the solution of nonhomogeneous linear constant coefficient differential equations. In addition, we will define the convolution integral and show. The use of laplace transforms to solve differential equations is presented along with detailed solutions. In this section we will examine how to use laplace transforms to solve ivp’s. Let us see.
(PDF) Laplace Transform and Systems of Ordinary Differential Equations
In this section we will examine how to use laplace transforms to solve ivp’s. One of the typical applications of laplace transforms is the solution of nonhomogeneous linear constant coefficient differential equations. Detailed explanations and steps are also included. We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. In addition, we will define.
Daily Chaos Laplace Transform Solving Differential Equation
In addition, we will define the convolution integral and show. Let us see how the laplace transform is used for differential equations. First let us try to find the laplace transform of a function that is a derivative. The use of laplace transforms to solve differential equations is presented along with detailed solutions. We will also give brief overview on.
Solving Differential Equations Using Laplace Transform Solutions dummies
The use of laplace transforms to solve differential equations is presented along with detailed solutions. In addition, we will define the convolution integral and show. We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. The examples in this section are restricted to differential equations that could be solved. First let us try to.
[differential equations] Laplace transform r/HomeworkHelp
In this section we will examine how to use laplace transforms to solve ivp’s. The use of laplace transforms to solve differential equations is presented along with detailed solutions. We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. In addition, we will define the convolution integral and show. The examples in this section.
(PDF) Laplace Transform and Systems of Ordinary Differential Equations
Detailed explanations and steps are also included. First let us try to find the laplace transform of a function that is a derivative. The examples in this section are restricted to differential equations that could be solved. In this section we will examine how to use laplace transforms to solve ivp’s. We will also give brief overview on using laplace.
Differential equations (Laplace transform Matchmaticians
The use of laplace transforms to solve differential equations is presented along with detailed solutions. In addition, we will define the convolution integral and show. First let us try to find the laplace transform of a function that is a derivative. In this section we will examine how to use laplace transforms to solve ivp’s. Let us see how the.
Let Us See How The Laplace Transform Is Used For Differential Equations.
The examples in this section are restricted to differential equations that could be solved. In addition, we will define the convolution integral and show. One of the typical applications of laplace transforms is the solution of nonhomogeneous linear constant coefficient differential equations. Detailed explanations and steps are also included.
First Let Us Try To Find The Laplace Transform Of A Function That Is A Derivative.
We will also give brief overview on using laplace transforms to solve nonconstant coefficient differential equations. The use of laplace transforms to solve differential equations is presented along with detailed solutions. In this section we will examine how to use laplace transforms to solve ivp’s.
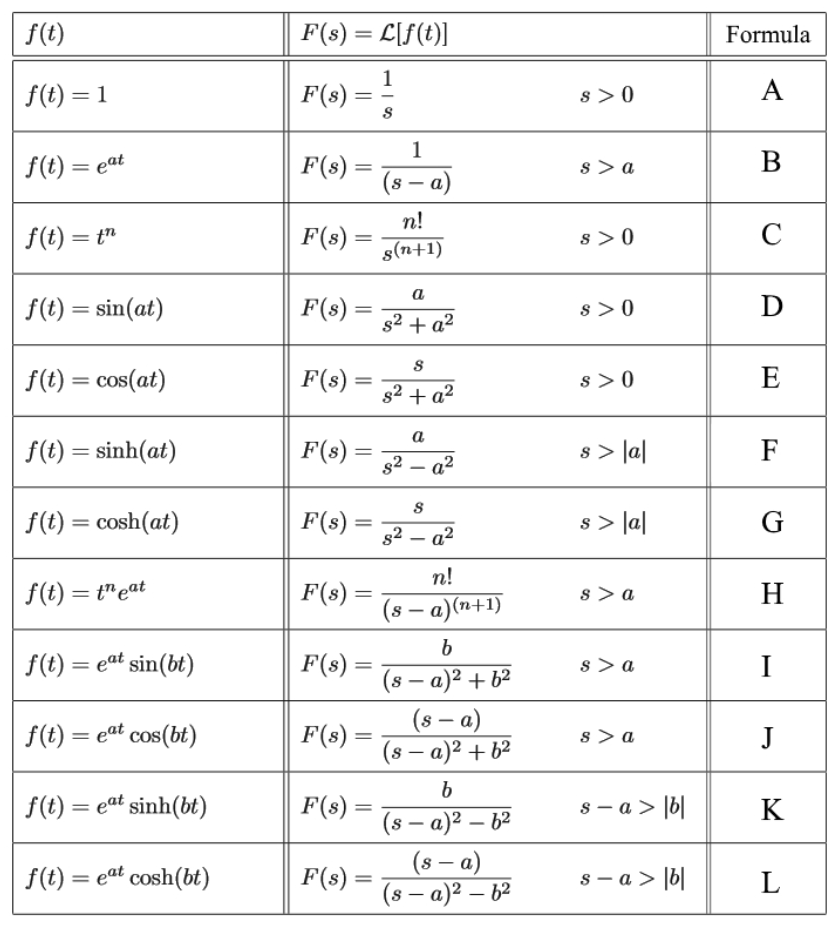





![[differential equations] Laplace transform r/HomeworkHelp](https://i.redd.it/d7gpew6q1gyc1.jpeg)

