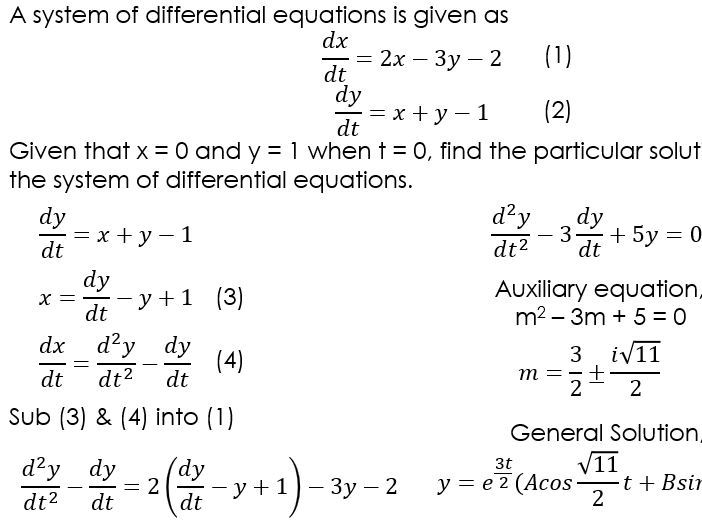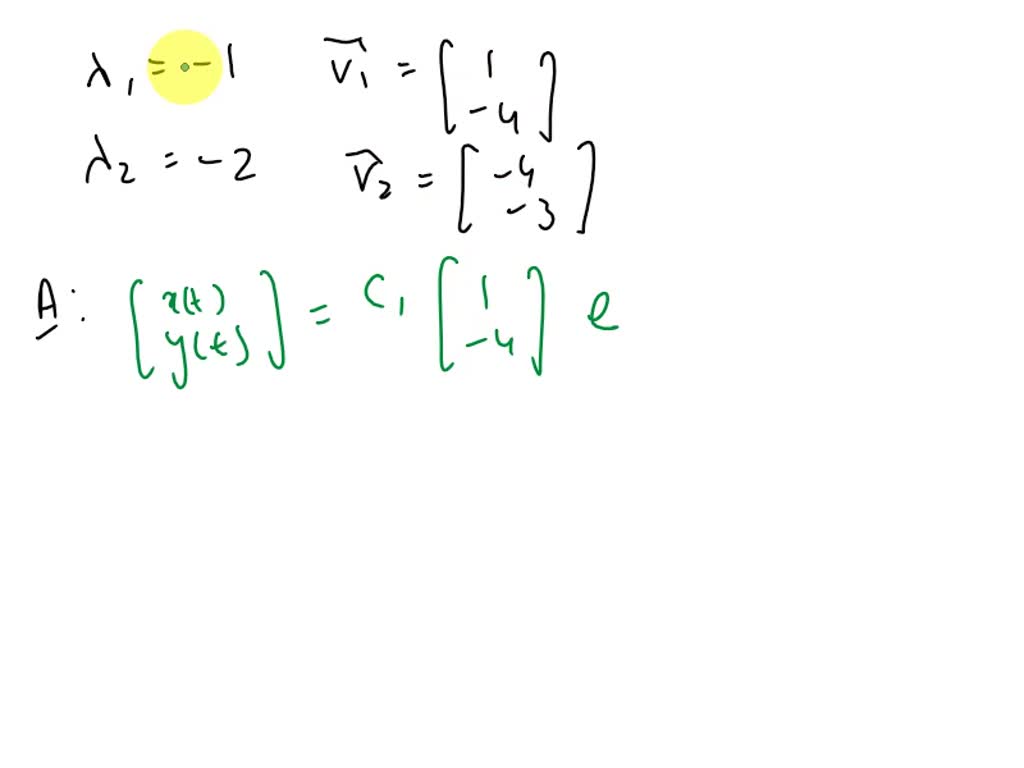Differential Equations Eigenvectors - This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. This is back to last week,. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. So lets’ solve ax = 2x: In this section we will introduce the concept of eigenvalues and eigenvectors of a. The pieces of the solution. (a − λi)→v = →0, and. This chapter ends by solving linear differential equations du/dt = au. But we need a method to compute eigenvectors. To find an eigenvector corresponding to an eigenvalue λ, we write.
But we need a method to compute eigenvectors. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This chapter ends by solving linear differential equations du/dt = au. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : (a − λi)→v = →0, and. So lets’ solve ax = 2x: This is back to last week,. To find an eigenvector corresponding to an eigenvalue λ, we write. In this section we will introduce the concept of eigenvalues and eigenvectors of a.
The pieces of the solution. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. This chapter ends by solving linear differential equations du/dt = au. But we need a method to compute eigenvectors. In this section we will introduce the concept of eigenvalues and eigenvectors of a. To find an eigenvector corresponding to an eigenvalue λ, we write. (a − λi)→v = →0, and. So lets’ solve ax = 2x: We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : Understanding eigenvalues and eigenvectors is essential for solving systems of differential.
(PDF) Differential Equations Review _ Eigenvalues & Eigenvectors
This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. But we need a method to compute eigenvectors. The pieces of the solution. (a − λi)→v = →0, and.
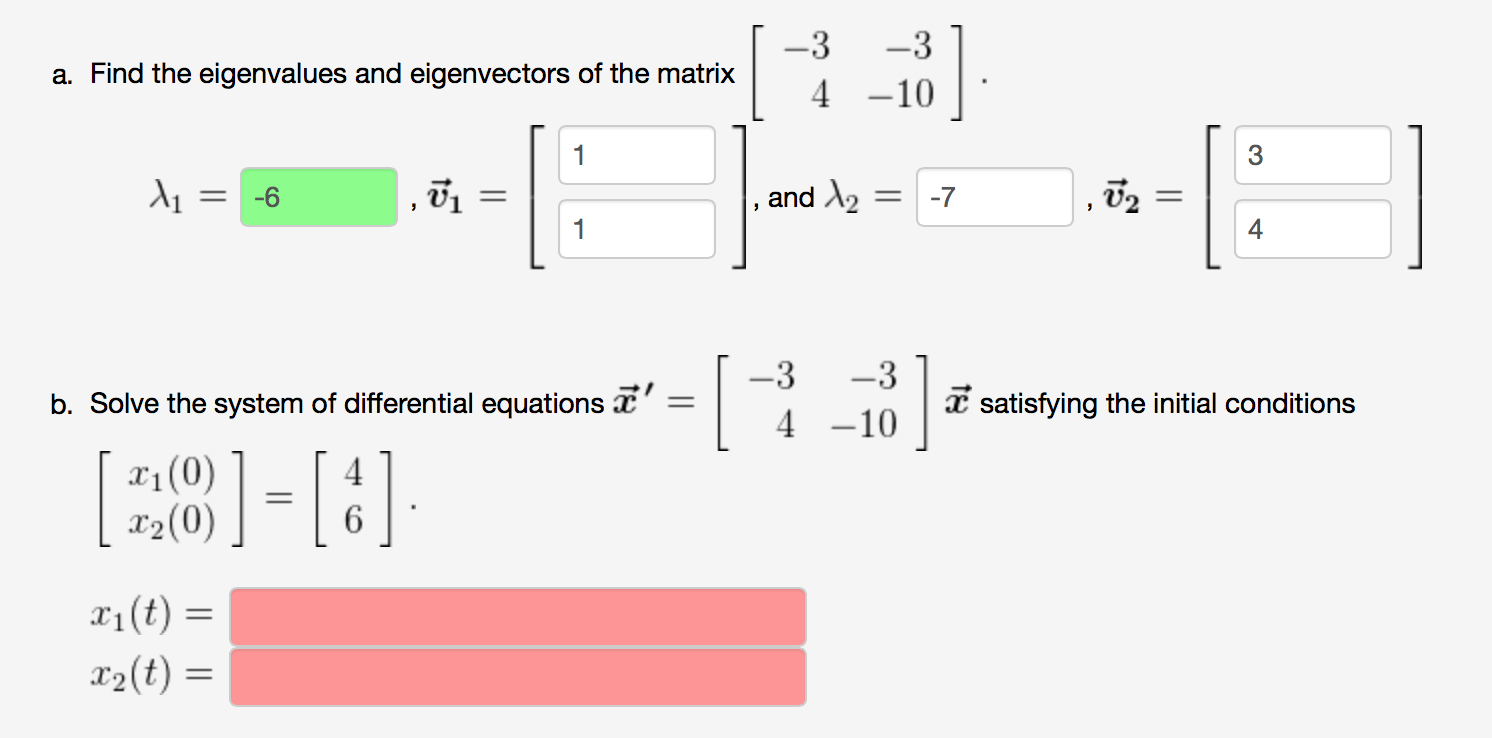
Solved a. Find the eigenvalues and eigenvectors of the
This is back to last week,. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. (a − λi)→v = →0, and. But we need a method to compute eigenvectors. In this section we will introduce the concept of eigenvalues and eigenvectors of a.
On Derivatives of Eigenvalues and Eigenvectors of The Download Free
But we need a method to compute eigenvectors. So lets’ solve ax = 2x: This is back to last week,. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
linear algebra Using eigenvectors and values to get systems of
(a − λi)→v = →0, and. To find an eigenvector corresponding to an eigenvalue λ, we write. But we need a method to compute eigenvectors. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
Differential Equation and Linear Algebra (MA11001) PDF Eigenvalues
To find an eigenvector corresponding to an eigenvalue λ, we write. So lets’ solve ax = 2x: The pieces of the solution. In this section we will introduce the concept of eigenvalues and eigenvectors of a. This is back to last week,.
Differential Equations Problems and Solutions Stability Theory
This chapter ends by solving linear differential equations du/dt = au. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. So lets’ solve ax = 2x: This is back to last week,. The pieces of the solution.
Solved Solve the given system of differential equations
The pieces of the solution. This chapter ends by solving linear differential equations du/dt = au. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. To find an eigenvector corresponding to an eigenvalue λ, we write. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) :
Modelling with differential equations Teaching Resources
This is back to last week,. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : (a − λi)→v = →0, and. So lets’ solve ax = 2x: This chapter ends by solving linear differential equations du/dt = au.
SOLVED Differential Equations Suppose that the matrix A has the
Understanding eigenvalues and eigenvectors is essential for solving systems of differential. But we need a method to compute eigenvectors. (a − λi)→v = →0, and. The pieces of the solution. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
Solved Application of eigenvalues and eigenvectors to
The pieces of the solution. This is back to last week,. In this section we will introduce the concept of eigenvalues and eigenvectors of a. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
This Section Introduces Eigenvalues And Eigenvectors Of A Matrix, And Discusses The Role.
In this section we will introduce the concept of eigenvalues and eigenvectors of a. To find an eigenvector corresponding to an eigenvalue λ, we write. This chapter ends by solving linear differential equations du/dt = au. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) :
Understanding Eigenvalues And Eigenvectors Is Essential For Solving Systems Of Differential.
The pieces of the solution. This is back to last week,. (a − λi)→v = →0, and. But we need a method to compute eigenvectors.