Differential Equations Eigenvalues And Eigenvectors - This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. The pieces of the solution. We've seen that solutions to linear odes have the form ert. In this section we will introduce the concept of eigenvalues and eigenvectors of a. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This chapter ends by solving linear differential equations du/dt = au. The concept of eigenvalues and eigenvectors. So we will look for solutions y1 = e ta. This short paper not only explains the connection between eigenvalues, eigenvectors and. Consider a linear homogeneous system of n.
Consider a linear homogeneous system of n. The concept of eigenvalues and eigenvectors. So we will look for solutions y1 = e ta. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. The pieces of the solution. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. In this section we will introduce the concept of eigenvalues and eigenvectors of a. This short paper not only explains the connection between eigenvalues, eigenvectors and. This chapter ends by solving linear differential equations du/dt = au. We've seen that solutions to linear odes have the form ert.
The pieces of the solution. We've seen that solutions to linear odes have the form ert. The concept of eigenvalues and eigenvectors. This chapter ends by solving linear differential equations du/dt = au. This short paper not only explains the connection between eigenvalues, eigenvectors and. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. So we will look for solutions y1 = e ta. In this section we will introduce the concept of eigenvalues and eigenvectors of a. Consider a linear homogeneous system of n. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
Solved Application of eigenvalues and eigenvectors to
Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. This short paper not only explains the connection between eigenvalues, eigenvectors and. We've seen that solutions to linear odes have the form ert. Consider a linear homogeneous system of n.
linear algebra Using eigenvectors and values to get systems of
So we will look for solutions y1 = e ta. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. Consider a linear homogeneous system of n. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This short paper not only explains the connection between eigenvalues, eigenvectors and.
(PDF) Linear Algebra Eigenvalues, Eigenvectors, and Differential
This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. The concept of eigenvalues and eigenvectors. Consider a linear homogeneous system of n. This chapter ends by solving linear differential equations du/dt = au. The pieces of the solution.
How to Find Eigenvalues and Eigenvectors 8 Steps (with Pictures)
This short paper not only explains the connection between eigenvalues, eigenvectors and. So we will look for solutions y1 = e ta. The pieces of the solution. The concept of eigenvalues and eigenvectors. We've seen that solutions to linear odes have the form ert.
Solved Solve the given system of differential equations
This short paper not only explains the connection between eigenvalues, eigenvectors and. The pieces of the solution. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. So we will look for solutions y1 = e ta. In this section we will introduce the concept of eigenvalues and eigenvectors of a.
eigenvalues eigenvectors Differential Equations Direction Field
Consider a linear homogeneous system of n. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. So we will look for solutions y1 = e ta. This short paper not only explains the connection between eigenvalues, eigenvectors and. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
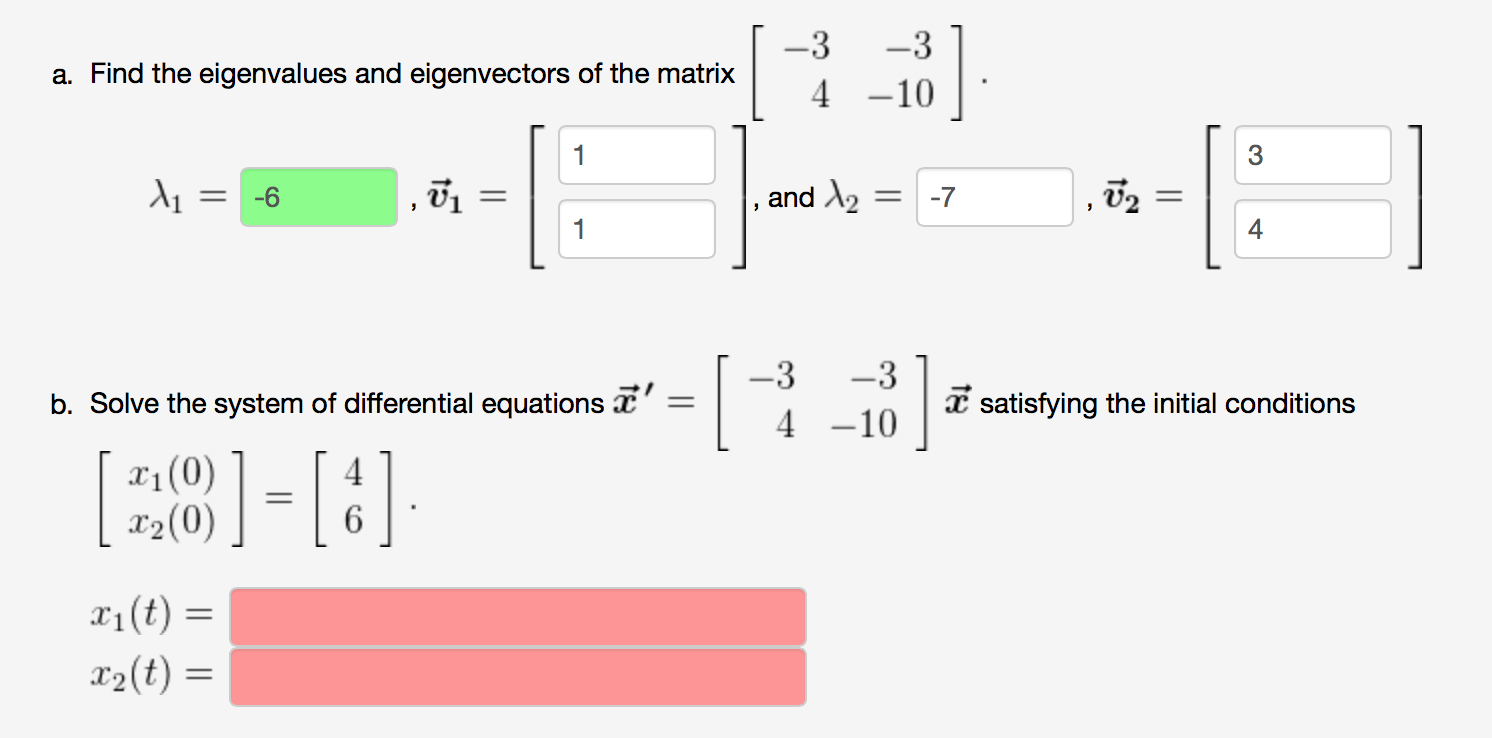
Solved a. Find the eigenvalues and eigenvectors of the
The pieces of the solution. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This chapter ends by solving linear differential equations du/dt = au. So we will look for solutions y1 = e ta. We've seen that solutions to linear odes have the form ert.
How to Find Eigenvalues and Eigenvectors 8 Steps (with Pictures)
So we will look for solutions y1 = e ta. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. In this section we will introduce the concept of eigenvalues and eigenvectors of a. The pieces of the solution. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
Solved (a) Using eigenvalues and eigenvectors, solve the
The pieces of the solution. Consider a linear homogeneous system of n. This chapter ends by solving linear differential equations du/dt = au. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. So we will look for solutions y1 = e ta.
(PDF) Differential Equations Review _ Eigenvalues & Eigenvectors
This short paper not only explains the connection between eigenvalues, eigenvectors and. Consider a linear homogeneous system of n. In this section we will introduce the concept of eigenvalues and eigenvectors of a. The pieces of the solution. This chapter ends by solving linear differential equations du/dt = au.
The Concept Of Eigenvalues And Eigenvectors.
We've seen that solutions to linear odes have the form ert. This short paper not only explains the connection between eigenvalues, eigenvectors and. The pieces of the solution. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
This Chapter Ends By Solving Linear Differential Equations Du/Dt = Au.
Understanding eigenvalues and eigenvectors is essential for solving systems of differential. Consider a linear homogeneous system of n. In this section we will introduce the concept of eigenvalues and eigenvectors of a. So we will look for solutions y1 = e ta.