Characteristic Equation Of Differential Equation - We can use ode theory to solve the characteristic equations, then piece together these. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. To evaluate the characteristic equation you have to consider only the homogeneous part:. Definition given a second order linear homogeneous differential. The characteristic equations are essential when solving linear homogeneous differential.
The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. Definition given a second order linear homogeneous differential. To evaluate the characteristic equation you have to consider only the homogeneous part:. We can use ode theory to solve the characteristic equations, then piece together these. The characteristic equations are essential when solving linear homogeneous differential.
To evaluate the characteristic equation you have to consider only the homogeneous part:. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. We can use ode theory to solve the characteristic equations, then piece together these. The characteristic equations are essential when solving linear homogeneous differential. Definition given a second order linear homogeneous differential.
First Order Differential Equation Worksheet Equations Worksheets
The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. To evaluate the characteristic equation you have to consider only the homogeneous part:. We can use ode theory to solve the characteristic equations, then piece together these. Definition given a second order linear homogeneous differential. The characteristic equations are essential when solving linear homogeneous differential.
Differential Equations Definition, Formula, Types, Examples
The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. Definition given a second order linear homogeneous differential. To evaluate the characteristic equation you have to consider only the homogeneous part:. The characteristic equations are essential when solving linear homogeneous differential. We can use ode theory to solve the characteristic equations, then piece together these.
Report on differential equation PPT
To evaluate the characteristic equation you have to consider only the homogeneous part:. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. We can use ode theory to solve the characteristic equations, then piece together these. The characteristic equations are essential when solving linear homogeneous differential. Definition given a second order linear homogeneous differential.
Solve the differential equation calculator sandwall
Definition given a second order linear homogeneous differential. We can use ode theory to solve the characteristic equations, then piece together these. The characteristic equations are essential when solving linear homogeneous differential. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. To evaluate the characteristic equation you have to consider only the homogeneous part:.
Solved 3. a) Solve the following differential equation using
The characteristic equations are essential when solving linear homogeneous differential. We can use ode theory to solve the characteristic equations, then piece together these. Definition given a second order linear homogeneous differential. To evaluate the characteristic equation you have to consider only the homogeneous part:. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic.
SOLVED A 9th order, linear, homogeneous, constant coefficient
The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. Definition given a second order linear homogeneous differential. The characteristic equations are essential when solving linear homogeneous differential. To evaluate the characteristic equation you have to consider only the homogeneous part:. We can use ode theory to solve the characteristic equations, then piece together these.
Solved (12 points) Suppose that the characteristic equation
To evaluate the characteristic equation you have to consider only the homogeneous part:. The characteristic equations are essential when solving linear homogeneous differential. We can use ode theory to solve the characteristic equations, then piece together these. Definition given a second order linear homogeneous differential. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic.
Ordinary differential equation PPT
To evaluate the characteristic equation you have to consider only the homogeneous part:. We can use ode theory to solve the characteristic equations, then piece together these. The characteristic equations are essential when solving linear homogeneous differential. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. Definition given a second order linear homogeneous differential.
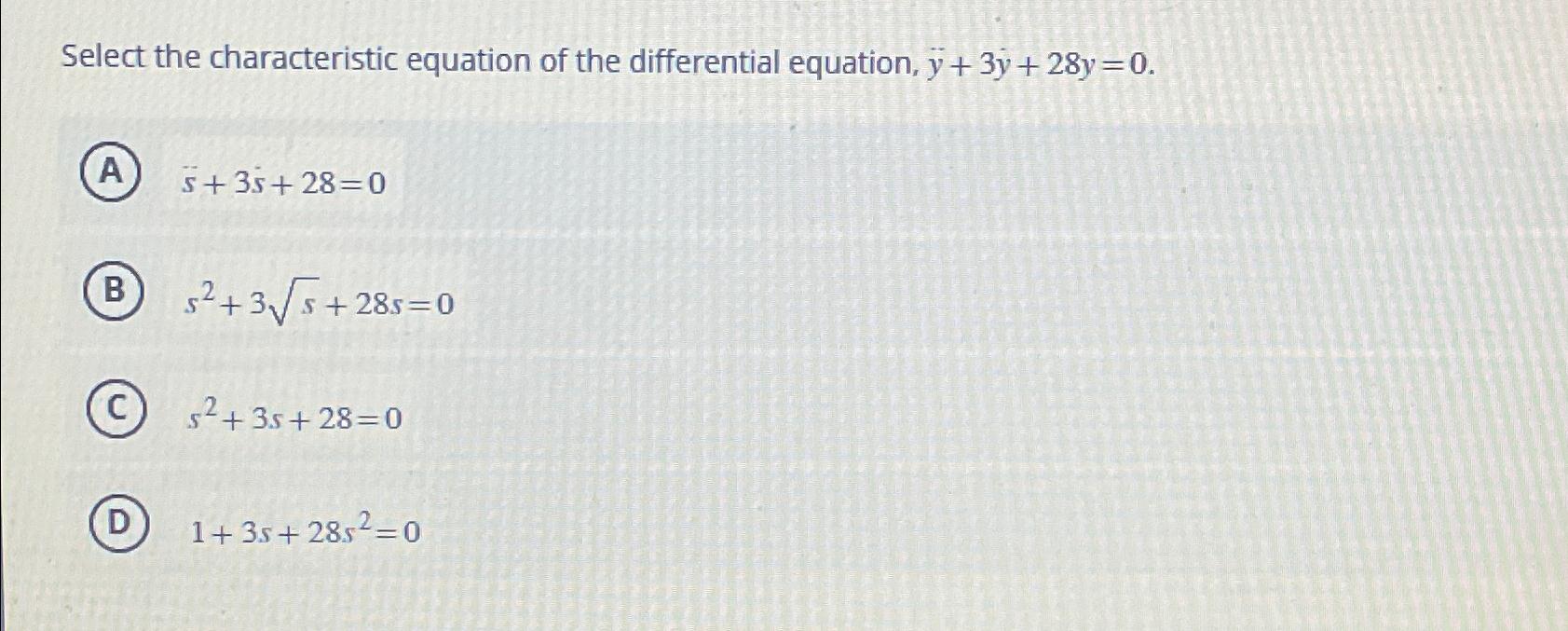
Solved Select the characteristic equation of the
We can use ode theory to solve the characteristic equations, then piece together these. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. Definition given a second order linear homogeneous differential. To evaluate the characteristic equation you have to consider only the homogeneous part:. The characteristic equations are essential when solving linear homogeneous differential.
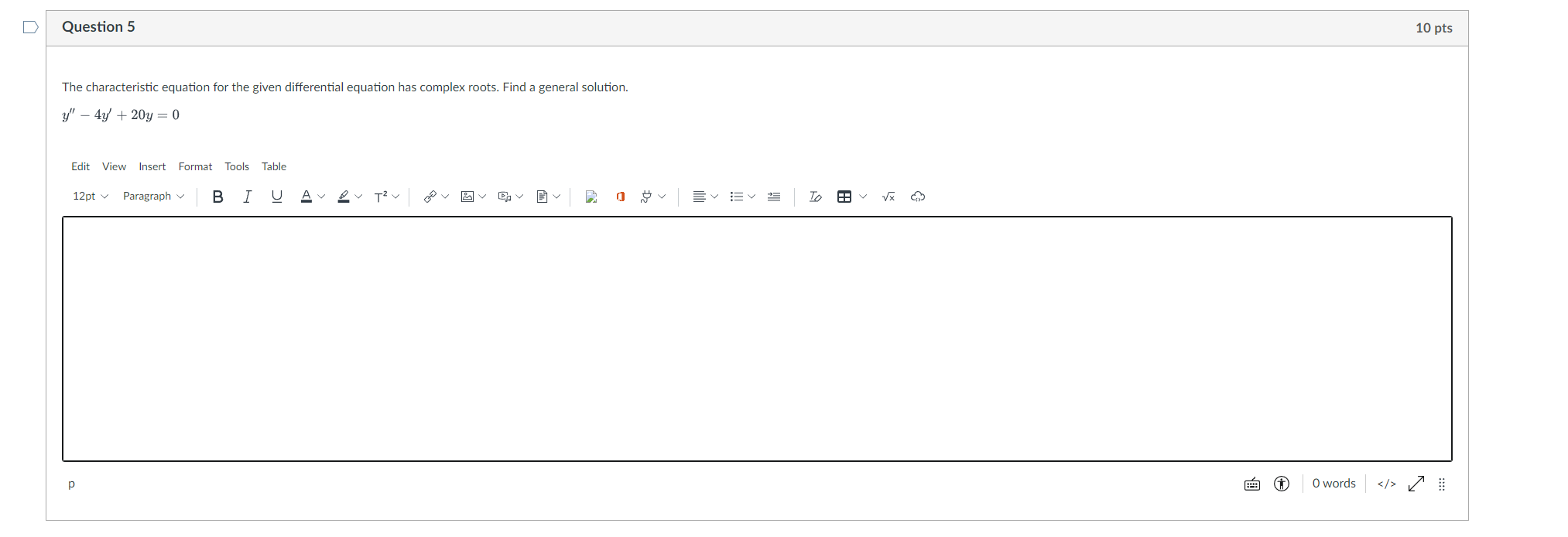
Solved The characteristic equation for the given
Definition given a second order linear homogeneous differential. We can use ode theory to solve the characteristic equations, then piece together these. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic. The characteristic equations are essential when solving linear homogeneous differential. To evaluate the characteristic equation you have to consider only the homogeneous part:.
The Characteristic Equations Are Essential When Solving Linear Homogeneous Differential.
To evaluate the characteristic equation you have to consider only the homogeneous part:. We can use ode theory to solve the characteristic equations, then piece together these. Definition given a second order linear homogeneous differential. The characteristic equation is \[{r^4} + 16 = 0\] so, a really simple characteristic.