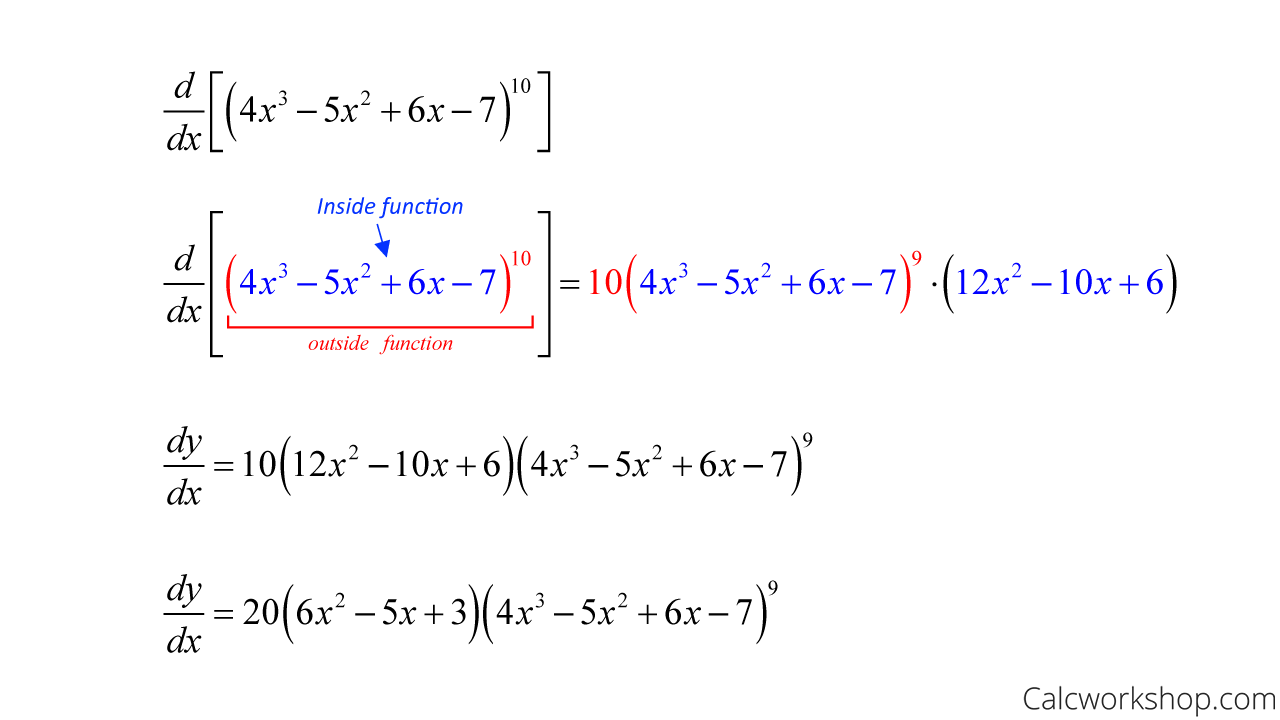Chain Rule Of Partial Differentiation - \frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. We can write the chain rule in way that is somewhat closer to the single variable. To implement the chain rule for two variables, we need six partial. The chain rule for total derivatives implies a chain rule for partial derivatives. To see how these work let’s go back and take a look at the chain rule for.
To implement the chain rule for two variables, we need six partial. To see how these work let’s go back and take a look at the chain rule for. \frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. We can write the chain rule in way that is somewhat closer to the single variable. The chain rule for total derivatives implies a chain rule for partial derivatives.
\frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. We can write the chain rule in way that is somewhat closer to the single variable. To see how these work let’s go back and take a look at the chain rule for. To implement the chain rule for two variables, we need six partial. The chain rule for total derivatives implies a chain rule for partial derivatives.
SOLUTION Implicit partial differentiation chain rule Studypool
We can write the chain rule in way that is somewhat closer to the single variable. To implement the chain rule for two variables, we need six partial. \frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. The chain rule for total derivatives implies a chain rule for partial derivatives. To see how these work let’s go back and take a.
THE CHAIN RULE IN PARTIAL DIFFERENTIATION 1 Simple chain
The chain rule for total derivatives implies a chain rule for partial derivatives. \frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. We can write the chain rule in way that is somewhat closer to the single variable. To implement the chain rule for two variables, we need six partial. To see how these work let’s go back and take a.
SOLUTION partial differentiation , partial derivatives , implicit
To implement the chain rule for two variables, we need six partial. We can write the chain rule in way that is somewhat closer to the single variable. The chain rule for total derivatives implies a chain rule for partial derivatives. To see how these work let’s go back and take a look at the chain rule for. \frac{\partial z}{\partial.
SOLUTION partial differentiation , partial derivatives , implicit
\frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. To implement the chain rule for two variables, we need six partial. We can write the chain rule in way that is somewhat closer to the single variable. The chain rule for total derivatives implies a chain rule for partial derivatives. To see how these work let’s go back and take a.
calculus Chain rule in partial derivatives Mathematics Stack Exchange
\frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. The chain rule for total derivatives implies a chain rule for partial derivatives. To implement the chain rule for two variables, we need six partial. We can write the chain rule in way that is somewhat closer to the single variable. To see how these work let’s go back and take a.
SOLUTION partial differentiation , partial derivatives , implicit
To implement the chain rule for two variables, we need six partial. To see how these work let’s go back and take a look at the chain rule for. We can write the chain rule in way that is somewhat closer to the single variable. The chain rule for total derivatives implies a chain rule for partial derivatives. \frac{\partial z}{\partial.
The Chain Rule Made Easy Examples and Solutions
\frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. The chain rule for total derivatives implies a chain rule for partial derivatives. To see how these work let’s go back and take a look at the chain rule for. To implement the chain rule for two variables, we need six partial. We can write the chain rule in way that is.
Partial derivatives chain rule clarification needed Mathematics Stack
The chain rule for total derivatives implies a chain rule for partial derivatives. \frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. We can write the chain rule in way that is somewhat closer to the single variable. To implement the chain rule for two variables, we need six partial. To see how these work let’s go back and take a.
Solved A question regarding the chain rule of partial
To implement the chain rule for two variables, we need six partial. We can write the chain rule in way that is somewhat closer to the single variable. The chain rule for total derivatives implies a chain rule for partial derivatives. To see how these work let’s go back and take a look at the chain rule for. \frac{\partial z}{\partial.
Chain Rule Differentiation Benytr
The chain rule for total derivatives implies a chain rule for partial derivatives. To see how these work let’s go back and take a look at the chain rule for. We can write the chain rule in way that is somewhat closer to the single variable. \frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. To implement the chain rule for.
To Implement The Chain Rule For Two Variables, We Need Six Partial.
The chain rule for total derivatives implies a chain rule for partial derivatives. We can write the chain rule in way that is somewhat closer to the single variable. \frac{\partial z}{\partial \theta }=\frac{\partial z}{\partial x}\,\frac{\partial x}{\partial \theta. To see how these work let’s go back and take a look at the chain rule for.