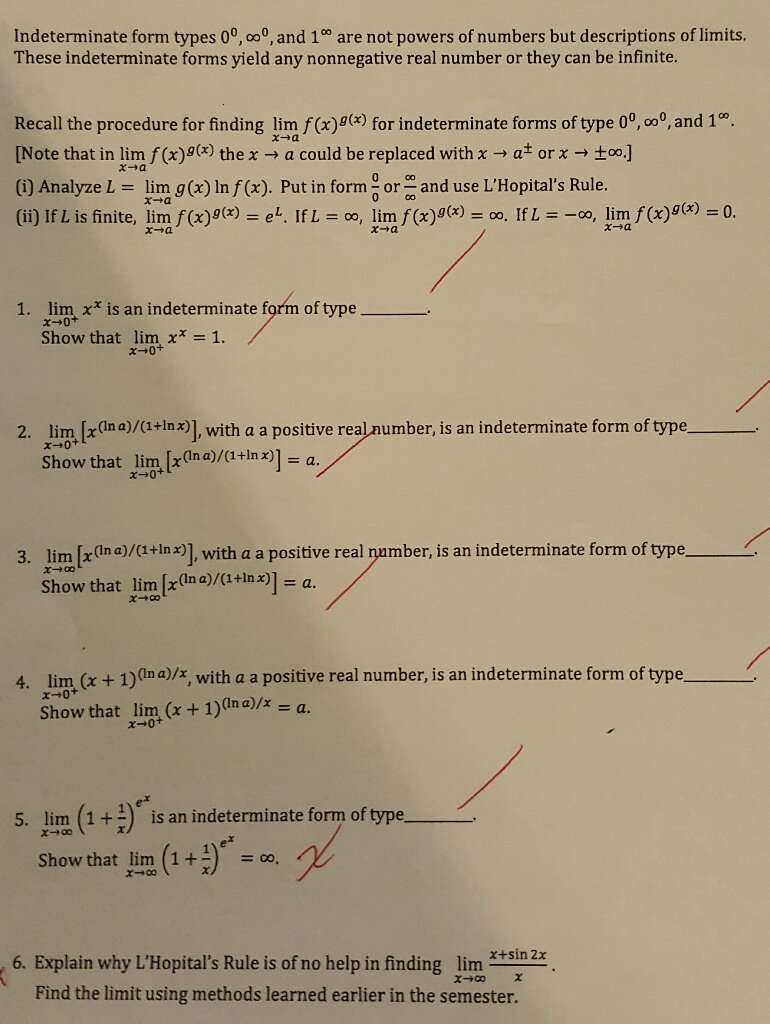0 Infinity Indeterminate Form - L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity.
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm.
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm.
Solved Which of the following limits are indeterminate
L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity.
Solved Show that 0 infinity is not an indeterminate form by
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm.
Explain in your own words why 0 infinity and 0
L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity.
Solved Seven Indeterminate Forms. An indeterminate form is a
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm.
Finding limit with indeterminate form 1^infinity r/askmath
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm.
PPT Indeterminate Forms PowerPoint Presentation, free download ID
L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity.
Solved Indeterminate form types 0 degree, infinity degree,
L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm. If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity.
Solved Identify the expression as an indeterminate form of
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm.
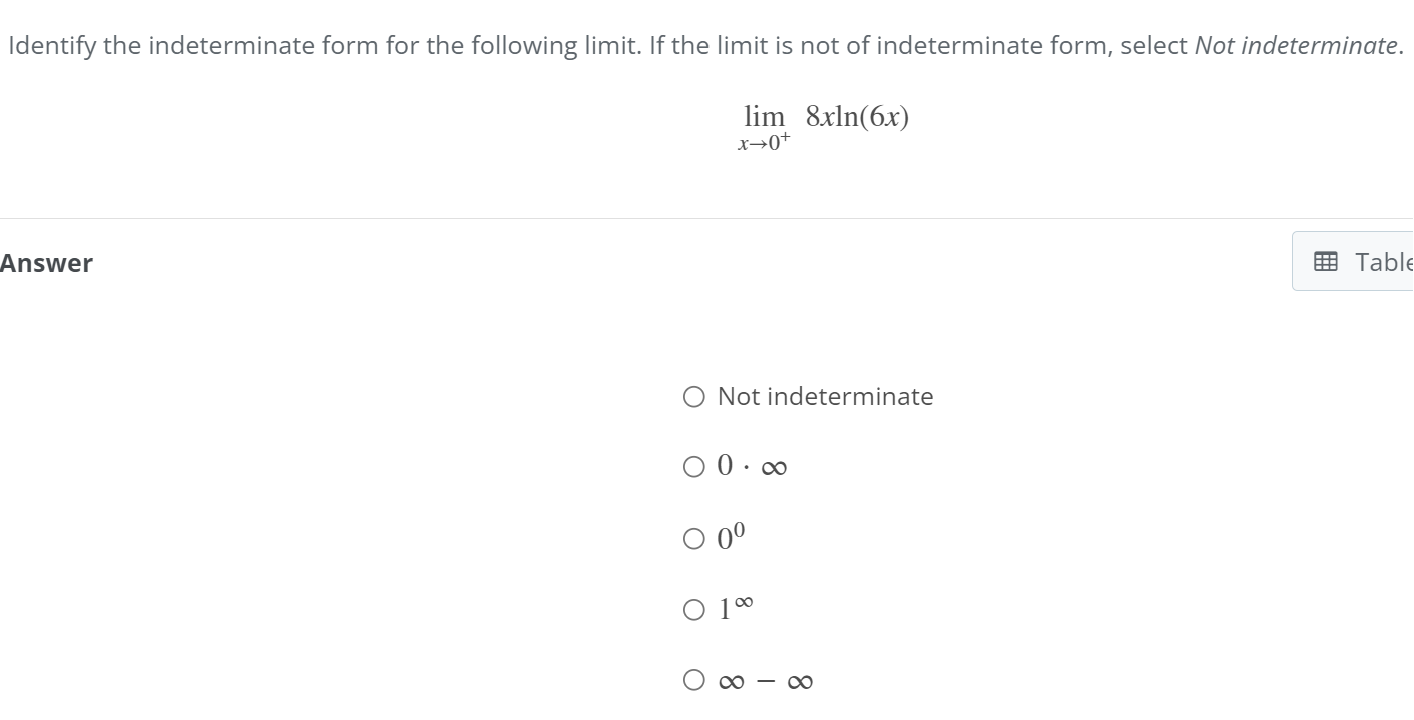
Solved Identify the indeterminate form for the following
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm.
Indeterminate form types 0^0, infinity^0, and
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity. L’hospital’s rule works great on the two indeterminate forms 0/0 and \({{ \pm.
L’hospital’s Rule Works Great On The Two Indeterminate Forms 0/0 And \({{ \Pm.
If $f(x)$ approaches $0$ from above, then the limit of $\frac{p(x)}{f(x)}$ is infinity.